ЬтФПФкШн
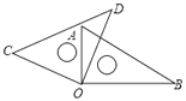
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЁЂBзјБъЗжБ№ЮЊAЃЈ0ЃЌaЃЉЁЂBЃЈbЃЌaЃЉЃЌЧвaЃЌbТњзуЃКЃЈa-3ЃЉ2+![]() =0ЃЌЯжЭЌЪБНЋЕуAЁЂBЗжБ№ЯђЯТЦНвЦ3ИіЕЅЮЛЃЌдйЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЗжБ№ЕУЕНЕуAЁЂBЕФЖдгІЕуCЁЂDЃЌСЌНгACЁЂBDЁЂABЃЎ
=0ЃЌЯжЭЌЪБНЋЕуAЁЂBЗжБ№ЯђЯТЦНвЦ3ИіЕЅЮЛЃЌдйЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЗжБ№ЕУЕНЕуAЁЂBЕФЖдгІЕуCЁЂDЃЌСЌНгACЁЂBDЁЂABЃЎ

ЃЈ1ЃЉЧѓЕуCЁЂDЕФзјБъМАЫФБпаЮABDCЕФУцЛ§SЫФБпаЮABDCЃЛ
ЃЈ2ЃЉдкyжсЩЯЪЧЗёДцдкЕуMЃЌСЌНгMCЁЂMDЃЌЪЙSЁїMCD=ЫФБпаЮABDCЃПШєДцдкетбљЕФЕуЃЌЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЕуPЪЧЯпЖЮBDЩЯЕФвЛИіЖЏЕуЃЌСЌНгPAЁЂPOЃЌЕБЕуPдкBDЩЯвЦЖЏЪБЃЈВЛгыBЁЂDжиКЯЃЉЃЌ![]() ЕФжЕЪЧЗёЗЂЩњБфЛЏЃЌВЂЫЕУїРэгЩЃЎ
ЕФжЕЪЧЗёЗЂЩњБфЛЏЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉSЫФБпаЮABDC=15ЃЛЃЈ2ЃЉДцдкЕуMЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ-6ЃЉЃЌЪЙSЁїMCD=SЫФБпаЮABDC ЃЌМћНтЮіЃЛЃЈ3ЃЉВЛБфЃЌМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩХМДЮЗНМАЫуЪѕЦНЗНИљЕФЗЧИКадПЩЧѓГіaЁЂbЕФжЕЃЌНјЖјМДПЩЕУГіЕуAЁЂBЕФзјБъЃЌдйИљОнЦНвЦЕФаджЪПЩЕУГіЕуCЁЂDЕФзјБъвдМАЫФБпаЮABDCЮЊЦНааЫФБпаЮЃЌЬзгУЦНааЫФБпаЮЕФУцЛ§ЙЋЪНМДПЩЧѓГіЫФБпаЮABDCЕФУцЛ§ЃЛ
ЃЈ2ЃЉЩшДцдкЕуMЃЈ0ЃЌyЃЉЃЌИљОнШ§НЧаЮЕФУцЛ§НсКЯSЁїMCD=SЫФБпаЮABDCЃЌМДПЩЕУГіЙигкyЕФКЌОјЖджЕЗћКХЕФвЛдЊвЛДЮЗНГЬЃЌНтжЎМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЙ§PЕузїPEЁЮABНЛOCгыEЕуЃЌИљОнЦНааЯпЕФаджЪЕУЁЯBAP+ЁЯDOP=ЁЯAPE+ЁЯOPE=ЁЯAPOЃЌЙЪБШжЕЮЊ1ЃЎ
НтЃКЃЈ1ЃЉЁпЃЈa-3ЃЉ2+![]() =0ЃЌ
=0ЃЌ
Ёрa=3ЃЌb=5ЃЌ
ЁрЕуAЃЈ0ЃЌ3ЃЉЃЌBЃЈ5ЃЌ3ЃЉЃЎ
НЋЕуAЃЌBЗжБ№ЯђЯТЦНвЦ3ИіЕЅЮЛЃЌдйЯђзѓЦНвЦ1ИіЕЅЮЛЃЌЕУЕНЕуCЁЂDЃЌ
ЁрЕуCЃЈ-1ЃЌ0ЃЉЃЌDЃЈ4ЃЌ0ЃЉЃЎ
гЩABЦНвЦЕУГіCDПЩжЊЃЌABЁЮCDЃЌЧвAB=CD=5ЃЌ
ЁрЫФБпаЮABDCЮЊЦНааЫФБпаЮЃЌ
ЁрSЫФБпаЮABDC=5ЁС3=15ЃЎ
ЃЈ2ЃЉЩшДцдкЕуMЃЈ0ЃЌyЃЉЃЌ
ИљОнЬтвтЕУЃКSЁїMCD=![]() ЁС5|y|=SЫФБпаЮABDC=15ЃЌ
ЁС5|y|=SЫФБпаЮABDC=15ЃЌ
Ёр![]() ЁС5|y|=15ЃЌНтЕУЃКy=ЁР6ЃЌ
ЁС5|y|=15ЃЌНтЕУЃКy=ЁР6ЃЌ
ЁрДцдкЕуMЃЈ0ЃЌ6ЃЉЛђЃЈ0ЃЌ-6ЃЉЃЌЪЙSЁїMCD=SЫФБпаЮABDCЃЎ
ЃЈ3ЃЉЕБЕуPдкBDЩЯвЦЖЏЪБЃЌ![]() =1ВЛБфЃЌРэгЩШчЯТЃК
=1ВЛБфЃЌРэгЩШчЯТЃК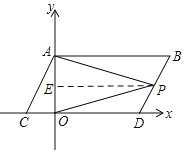
Й§ЕуPзїPEЁЮABНЛOAгкEЃЎ
ЁпCDгЩABЦНвЦЕУЕНЃЌдђCDЁЮABЃЌ
ЁрPEЁЮCDЃЌ
ЁрЁЯBAP=ЁЯAPEЃЌЁЯDOP=ЁЯOPEЃЌ
ЁрЁЯBAP+ЁЯDOP=ЁЯAPE+ЁЯOPE=ЁЯAPOЃЌ
Ёр![]() =1ЃЎ
=1ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГаТЕъПЊвЕаћДЋЃЌНјЕъгаРёЛюЖЏЃЌЕъдБУЧашзМБИжЦзїдВжљЬхРёЦЗжНКаЃЈШчЭМЂйЃЉЃЌУПИіжНКагЩ1ИіГЄЗНаЮВрУцКЭ2ИідВаЮЕзУцзщГЩЃЌЯжга100еХе§ЗНаЮжНАхШЋВПвдAЛђепBЗНЗЈНиМєжЦзїЃЈШчЭМЂкЃЉЃЌЩшНиМєЪБxеХгУAЗНЗЈЃЎ

ЃЈ1ЃЉИљОнЬтвтЃЌЭъГЩвдЯТБэИёЃК
ВУМєЗЈA | ВУМєЗЈB | |
ГЄЗНаЮВрУц | x | ЁЁ ЁЁ |
дВаЮЕзУц | ЁЁ ЁЁ | 0 |
ЃЈ2ЃЉШєВУМєГіЕФГЄЗНаЮВрУцКЭдВаЮЕзУцЧЁКУгУЭъЃЌЮЪФмзіЖрЩйИіжНКаЃП
ЃЈ3ЃЉАДвдЩЯжЦзїЗНЗЈЃЌШєЕъдБУЧЯЃЭћзМБИ300ИіРёКаЃЌФЧжСЩйЛЙашвЊе§ЗНаЮжНАхЁЁ ЁЁеХЃЎ