题目内容
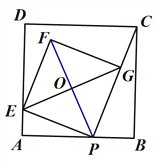
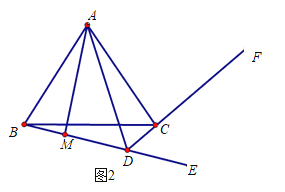
【题目】如图,在菱形ABCD中,tan∠ABC=![]() ,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则
,P为AB上一点,以PB为边向外作菱形PMNB,连结DM,取DM中点E,连结AE,PE,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:如图,延长AE交MP的延长线于F,作AH⊥PF于H.证明△AED≌△FEM,可得AE=EF.AD=MF=AB,由PM=PB,推出PA=PF,推出PE⊥AF,∠APE=∠FPE,由∠APF=∠ABC,可得tan∠APE=tan∠ABC=![]() =
=![]() ,设AH=4k,PH=3k,解直角三角形求出AE、PE即可解决问题.
,设AH=4k,PH=3k,解直角三角形求出AE、PE即可解决问题.
详解:如图,延长AE交MP的延长线于F,作AH⊥PF于H.
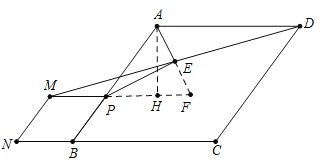
∵AD∥CN∥PM,∴∠ADE=∠EMF.∵ED=EM,∠AED=∠MEF,∴△AED≌△FEM,∴AE=EF.AD=MF=AB.∵PM=PB,∴PA=PF,∴PE⊥AF,∠APE=∠FPE.∵∠APF=∠ABC,∴tan∠APE=tan∠ABC=![]() =
=![]() ,设AH=4k,PH=3k,则PA=PF=5k,FH=2k,AF=
,设AH=4k,PH=3k,则PA=PF=5k,FH=2k,AF=![]() =2
=2![]() k.∵
k.∵![]() PFAH=
PFAH=![]() AFPE,∴PE=2
AFPE,∴PE=2![]() k,AE=
k,AE=![]() k
k
∴AE:PE=![]() k:2
k:2![]() =1:2.
=1:2.
故选C.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目