题目内容
【题目】如图,抛物线y=a( x+1 )2-4a(a<0)与x轴交于点A、B(A在B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,连接BD交抛物线的对称轴于点E,连接BC、CE.
(1)抛物线顶点坐标为 (用含a的代数式表示),A点坐标为 ,
(2)当△DCE的面积为![]() 时,求a的值;
时,求a的值;
(3)当△BCE为直角三角形时,求抛物线的解析式.

【答案】(1)(-1,-4a),(-3,0)(2)-![]() (3)y=-( x+1 )2+4或y=-
(3)y=-( x+1 )2+4或y=-![]() ( x+1 )2 +
( x+1 )2 +![]()
【解析】分析:(1)由抛物线的性质,直接得到顶点坐标.令y=0,即可求得A点坐标.
(2)设对称轴交CD于M,交x轴于F,得到C(0,-3a).由对称轴为直线x=1,得到D(-2,-3a),由△DCE的面积=![]() ,得到ME的长,即可得到E的坐标,易求直线BD的解析式为:
,得到ME的长,即可得到E的坐标,易求直线BD的解析式为:![]() .由E为直线BD与对称轴的交点,即可得到a的值.
.由E为直线BD与对称轴的交点,即可得到a的值.
(3)作DH⊥x轴于H.显然,∠CBE为锐角,所以∠CBE![]() 90°.分两种情况讨论:
90°.分两种情况讨论:
①若∠BEC=90°,②若∠BCE=90°。
详解:(1)抛物线y=a( x+1 )2-4a(a<0)的顶点坐标是(-1,-4a).令y=0,得:a( x+1 )2-4a=0,解得:x=-3,或x=1,∴A点坐标为(-3,0).
(2)设对称轴交CD于M,交x轴于F.令x=0,得:y=a-4a=-3a,∴C(0,-3a).∵对称轴为直线x=1,∴D(-2,-3a),∴DC=2.∵△DCE的面积=![]() ,∴
,∴![]() DCME=
DCME=![]() ,∴ME=
,∴ME=![]() ,∴E(-1,
,∴E(-1,![]() ),易求直线BD的解析式为:
),易求直线BD的解析式为:![]() .∵E为直线BD与对称轴的交点,∴当x=-1时,y=-2a,∴-2a=
.∵E为直线BD与对称轴的交点,∴当x=-1时,y=-2a,∴-2a=![]() ,解得:a=
,解得:a=![]() .
.
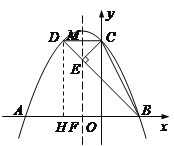
(3)作DH⊥x轴于H.
显然,∠CBE为锐角,所以∠CBE![]() 90°.
90°.
①若∠BEC=90°,则∠DEC=90°.
∵CD∥x轴,∴由对称性可知∠CEM=∠DEM=45°,∴∠BEF=45°,∴∠BDH=45°,∴BH=DH.
∵y=a( x+1 )2-4a,∴A(-3,0),B(1,0),C(0,-3a),抛物线的对称轴为直线x=-1,∴D(-2,-3a),∴BH=3,DH=-3a,∴a=-1∴y=-( x+1 )2+4;
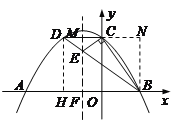
②若∠BCE=90°,作BN⊥DC交DC的延长线于N,则∠BCN+∠ECM=∠BCN+∠EDM=∠BDH+∠EDM=90°,∴∠BCN=∠BDH,∴Rt△BCN∽Rt△BDH,∴BN:CN=BH:DH ,∴-3a:1=3:-3a,∴a=![]() ,∴ y=
,∴ y=![]() ( x+1 )2 .
( x+1 )2 .
综上所述:y=-( x+1 )2+4或![]() .
.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案