题目内容
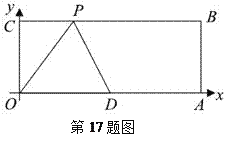
【题目】如图所示,![]() ,
,![]() 分别表示使用一种白炽灯和一种节能灯的费用
分别表示使用一种白炽灯和一种节能灯的费用![]() (元,分别用y1与y2表示)与照明时间
(元,分别用y1与y2表示)与照明时间![]() (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.
(1)根据图象分别求出![]() ,
,![]() 对应的函数(分别用y1与y2表示)关系式;
对应的函数(分别用y1与y2表示)关系式;
(2)对于白炽灯与节能灯,请问该选择哪一种灯,使用费用会更省?

【答案】(1)y1=![]() x+2,y2=
x+2,y2=![]() x+20(2)见解析
x+20(2)见解析
【解析】
(1)由图像可知,l1的函数为一次函数,则设y1=k1x+b1.由图象知,l1过点(0,2)、(500,17),能够得出l 1的函数解析式.同理可以得出l2的函数解析式.
(2)由图像可知l1、 l2的图像交于一点,那么交点处白炽灯和节能灯的费用相同,即![]() x+2=
x+2=![]() x+20,由此得出x=1000时费用相同;x<1000时,使用白炽灯省钱;x>1000时,使用节能灯省钱.
x+20,由此得出x=1000时费用相同;x<1000时,使用白炽灯省钱;x>1000时,使用节能灯省钱.
(1)设l1的函数解析式为y1=k1x+b1,
由图象知,l1过点(0,2)、(500,17),
可得方程组 ,解得
,解得 ,
,
故,l1的函数关系式为y1=![]() x+2;
x+2;
设l2的函数解析式为y2=k2x+b2,
由图象知,l2过点(0,20)、(500,26),
可得方程组 ,解得
,解得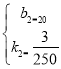 ,
,
y2=![]() x+20;
x+20;
(2)由题意得,![]() x+2=
x+2=![]() x+20,解得x=1000,
x+20,解得x=1000,
故,①当照明时间为1000小时时,两种灯的费用相同;
②当照明时间超过1000小时,使用节能灯省钱.
③当照明时间在1000小时以内,使用白炽灯省钱.

练习册系列答案
相关题目