Question

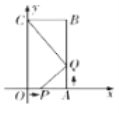
【题目】图中的每个小正方形的边长均为1，每个小正方形的顶点叫做格点．线段和的端点均在格点上．

（1）在图中画出以为一边的，点在格点上，使的面积为4，且的一个角的正切值是；

（2）在图中画出以为顶角的等腰（非直角三角形），点在格点上．请你直接写出的面积．

Answer 1

【答案】（1）画图见解析；（2）画图见解析，6．

【解析】

（1）根据AB的长以及△ABE的面积可得出AB边上的高为2，再直接利用正切的定义借助网格得出E点位置，再画出△ABE即可；
（2）在网格中根据勾股定理可得出DC2=22+42，利用网格找出使CF2=DC2=22+42的点F即可，然后利用网格通过转化法可求出△CDF的面积．

解：（1）设△ABE中AB边上的高为EG，则S△ABE=×AB×EG=4，

又AB=4，∴EG=2，

假设∠A的正切值为，即tanA=，∴AG=6，

∴点E的位置如图所示，△ABE即为所求：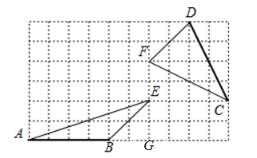

（2）根据勾股定理可得，DC2=22+42，∴CF2=DC2=22+42，

所以点F的位置如图所示，△DCF即为所求；
根据网格可得，△DCF的面积=4×4-×2×4-×2×4-×2×2=6．