题目内容
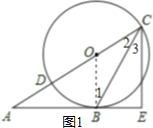
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
【答案】
【解析】试题分析:(1)证明:如图1,连接OB,由AB是⊙0的切线,得到OB⊥AB,由于CE丄AB,的OB∥CE,于是得到∠1=∠3,根据等腰三角形的性质得到∠1=∠2,通过等量代换得到结果.
(2)如图2,连接BD通过△DBC∽△CBE,得到比例式![]() ,列方程可得结果.
,列方程可得结果.
(1)证明:如图1,连接OB,
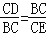
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE丄AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图2,连接BD,
∵CE丄AB,
∴∠E=90°,
∴BC=![]() =
=![]() =5,
=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴![]() ,
,
∴BC2=CDCE,
∴CD=![]() =
=![]() ,
,
∴OC=![]() =
=![]() ,
,
∴⊙O的半径=![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?




