��Ŀ����
����Ŀ����ɫֲ�����۹�˾��������ijƷ�ֵ�����Ҷֲ�������������������Ҷֲ���������г�����������������ź���ͼ������ͼ��Ϊһ��ֱ�ߣ�ͼ��Ϊһ�������ߣ��������߶���Ϊ(6��1)�������ͼ�����������⣺
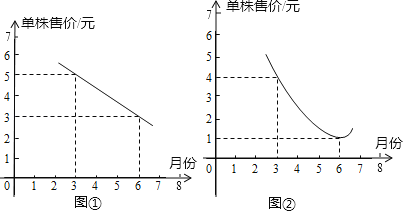
��1�������˾��3�·�������������Ҷֲ�����������������Ԫ��
��2����ֱ��д��ͼ�����ֱ�ߵĽ���ʽ��
��3�����������˾���ĸ���������������Ҷֲ������������������ע����������������ۼ۩�����ɱ���
���𰸡���1��1����2��y1����![]() x+7����3��5����������ֲ�����������
x+7����3��5����������ֲ�����������
��������
��1������ͼ����3�·��ۼ�Ϊ5Ԫ������ͼ����3�·ݵijɱ�Ϊ4Ԫ����ÿ�����Ϊ5��4��1��Ԫ����������⣻
��2���㣨3��5������6��3��Ϊһ�κ����ϵĵ㣬���ֱ�ߵı���ʽΪ��y1����![]() x+7��
x+7��
��3�����y2�Ľ���ʽ�����y1��y2��ֵ���䷽�ɵý��ۣ�
��1������ͼ����3�·��ۼ�Ϊ5Ԫ������ͼ����3�·ݵijɱ�Ϊ4Ԫ����ÿ�����Ϊ5��4��1��Ԫ����
�ʴ�Ϊ��1��
��2����ֱ�ߵı���ʽΪ��y1��kx+b��k��0����
�ѵ㣨3��5������6��3��������ʽ�ã�![]() ��
��
��ã�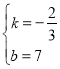 ��
��
��ֱ�ߵı���ʽΪ��y1����![]() x+7��
x+7��
��3���裺�����ߵı���ʽΪ��y2��a��x��m��2+n��
�߶���Ϊ��6��1������������ʽΪ��y2��a��x��6��2+1��
�ѵ㣨3��4��������ʽ�ã�
4��a��3��6��2+1����ã�a��![]() ��
��
�������ߵı���ʽΪ��y2��![]() ��x��6��2+1��
��x��6��2+1��
�ʴ�Ϊ��y1����![]() x+7��y2��
x+7��y2��![]() ��x��6��2+1��
��x��6��2+1��
��3��y1��y2����![]() x+7��
x+7��![]() ��x��6��2��1����
��x��6��2��1����![]() ��x��5��2+
��x��5��2+![]() ��
��
��a����![]() ��0��
��0��
��x��5ʱ������ȡ�����ֵ��
�ʣ�5����������ֲ�����������