题目内容
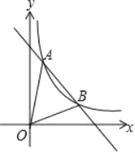
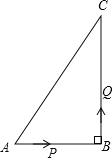
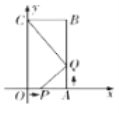
【题目】如图,四边形OABC是矩形,点A坐标为(2,0),点C坐标为(0,4).点P从点O出发,沿OA以每秒1个单位长度的速度向点A运动,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当△CBQ与△PAQ相似时,求出t的值;
(2)当t=1时,抛物线y=2x2+bx+c经过P,Q两点,与y轴交于点M,在该抛物线上找点D,使∠MQD=![]() ∠MPQ,求点D的坐标.
∠MPQ,求点D的坐标.
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或
或![]()
【解析】
(1)根据矩形的性质得:∠B=∠PAQ=90![]() ,所以当△CBQ与△PAQ相似时,存在两种情况:①当△PAQ∽△QBC时,
,所以当△CBQ与△PAQ相似时,存在两种情况:①当△PAQ∽△QBC时,![]() ,②当△PAQ∽△CBQ时,
,②当△PAQ∽△CBQ时,![]() ,分别列方程可得t的值;
,分别列方程可得t的值;
(2)根据t=1求抛物线的解析式,根据Q(2,2),M(0,2),可得MQ∥x轴,则PM=PQ,PE⊥MQ,画出符合条件的点D,利用三角函数,列比例式可得点D的坐标,同理根据对称可得另一个点D.
(1)如图1,
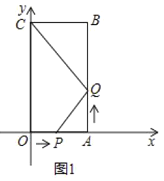
∵当点P与点A重合时运动停止,且△PAQ可以构成三角形,
∴0<t<2,
∵四边形OABC是矩形,
∴∠B=∠PAQ=90![]()
∴当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,
![]() ,
,
∴![]() ,
,
4t210t+4=0,
(4t2)(t2)=0,
t1=2(舍),t2=![]() ,
,
②当△PAQ∽△CBQ时,![]() ,
,
∴![]() ,
,
t26t+4=0,
t=![]() ,
,
∵![]() >2,
>2,
∴t=![]() 不符合题意,舍去,
不符合题意,舍去,
综上所述,当△CBQ与△PAQ相似时,t的值是![]() 或
或![]() ;
;
(3)当t=1时,P(1,0),Q(2,2),
把P(1,0),Q(2,2)代入抛物线y=2x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
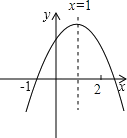
∴抛物线:y=2x24x+2=2(x1)2,
∴顶点为P(1,0),
∵Q(2,2),M(0,2),
∴MQ∥x轴,
作抛物线对称轴,交MQ于E,设DQ交y轴于H,
∴PM=PQ,PE⊥MQ,
∴∠MPE=∠QPE=![]() ∠MPQ,
∠MPQ,
如图2,∠MQD=![]() ∠MPQ=∠QPE,
∠MPQ=∠QPE,
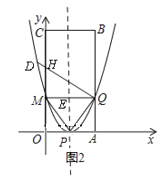
∴tan∠MQD=tan∠QPE=![]() ,
,
即![]() ,MH=1,
,MH=1,
∴H(0,3),Q(2,2)
设HQ的解析式为y=kx+b
把H(0,3),Q(2,2)代入得![]() ,解得
,解得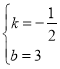
∴y= ![]() x+3,
x+3,
则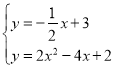
![]() ,
,
解得:x1=2(舍),x2= ![]() ,
,
∴D![]() ;
;
同理,在M的下方,y轴上存在点H,如图3,使∠HQM=![]() ∠MPQ=∠QPE,
∠MPQ=∠QPE,
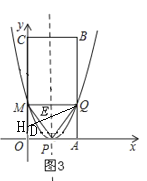
由对称性得:H(0,1),
设HQ的解析式为y=px+q
把H(0,1),Q(2,2)代入得![]() ,解得
,解得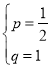
∴y=![]() x+1,
x+1,
∴HQ的解析式:y=![]() x+1,
x+1,
则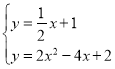 ,
,
![]() ,
,
解得:x1=2(舍),x2=![]() ,
,
∴D![]() ;
;
综上所述,点D的坐标为:D![]() 或
或![]() .
.