题目内容
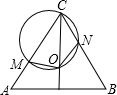
等边三角形ABC的边长是4
,三角形内有一点O,且OA=OB=OC,则OA=______.
| 3 |
∵OA=OB=OC,
∴O为△ABC三边垂直平分线的交点,
∴OB为∠ABC的角平分线,
∴∠OBD=30°,
∴OB=OD,
∵BD=
BC=2
.
∴BD=
=2
,
即
OD=2
,
∴OB=2OD=4.
故答案为4.
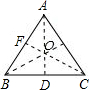
∴O为△ABC三边垂直平分线的交点,
∴OB为∠ABC的角平分线,
∴∠OBD=30°,
∴OB=OD,
∵BD=
| 1 |
| 2 |
| 3 |
∴BD=
| OB2-OD2 |
| 3 |
即
| 3 |
| 3 |
∴OB=2OD=4.
故答案为4.


练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目