Question

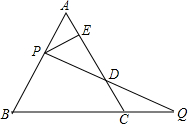
如图，点P是等腰△ABC的底边BC上的点，以AP为腰在AP的两侧分别作等腰△AFP和等腰△AEP，且∠APF=∠APE=∠B，PF交AB于点M，PE交AC于点N，连接MN．
求证：MN∥BC．

Answer 1

证明：∵△ABC、△AFP和△AEP是等腰三角形，
∴AF=AP，∠F=∠APN，∠FAM=∠PAN，
在△AFM和△APN中，
∵

∠F=∠APN AF=AP ∠FAM=∠PAN

∴△AFM≌△APN（ASA），
∴AM=AN．
∴∠AMN=∠B，
∴MN∥BC．