题目内容
如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.
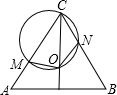

证明:如图,连接AO,(1分)
在△AMO和△CNO中,AM=CN=1,
∵直线CO是正△ABC的一条对称轴,
∴∠ACO=∠NCO.
∴MO=NO.
又∠AMO=∠CNO,
∴△AMO≌△CNO.(5分)
∴∠MAO=∠NCO=30°.
∴O是正△ABC两个内角平分线的交点.
∴点O是正△ABC的中心.(7分)

在△AMO和△CNO中,AM=CN=1,
∵直线CO是正△ABC的一条对称轴,
∴∠ACO=∠NCO.
∴MO=NO.
又∠AMO=∠CNO,
∴△AMO≌△CNO.(5分)
∴∠MAO=∠NCO=30°.
∴O是正△ABC两个内角平分线的交点.
∴点O是正△ABC的中心.(7分)


练习册系列答案
相关题目