题目内容
正三角形OAB的顶点O是原点，A点坐标是（-2，0），B点在第二象限，则B点的坐标是______．
过点B作BC⊥AO于点C，
∵正三角形OAB的顶点O是原点，A点坐标是（-2，0），B点在第二象限，
∴AO=AB=BO=2，
∵BC⊥AO，
∴∠CBO=30°，CO=AC=1，
∴BC=BOcos30°=
，
则B点的坐标是：（-1，
）．
故答案为：（-1，
）．
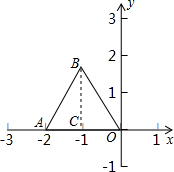
∵正三角形OAB的顶点O是原点，A点坐标是（-2，0），B点在第二象限，
∴AO=AB=BO=2，
∵BC⊥AO，
∴∠CBO=30°，CO=AC=1，
∴BC=BOcos30°=
| 3 |
则B点的坐标是：（-1，
| 3 |
故答案为：（-1，
| 3 |
练习册系列答案
世纪百通期末金卷系列答案
相关题目
