题目内容
【题目】甲、乙两车分别从![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到![]() 地,乙车匀速前往
地,乙车匀速前往![]() 地.设甲、乙两车距
地.设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() (小时),
(小时),![]() 与
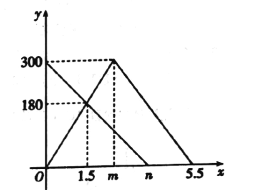
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
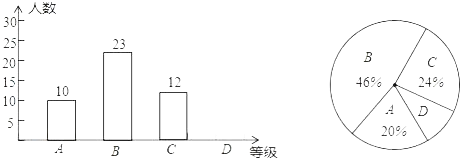
(1)图中,![]() ,
,![]() ;
;
(2)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在甲车返回到![]() 地的过程中,当
地的过程中,当![]() 为何值时,甲、乙两车相距190千米?
为何值时,甲、乙两车相距190千米?
【答案】(1)2.5,3.75;(2)y=-100x+550(2.5≤x≤5.5);(3)3.
【解析】
(1)根据路程、速度、时间之间的关系,即可解答;
(2)根据路程、速度、时间之间的关系,设甲车返回时y与x之间的函数关系式为y=kx+b,把点代入解析式进行计算即可解答;
(3)首先求出甲的速度:![]() ,乙的速度:
,乙的速度:![]() ,再根据在甲车返回到
,再根据在甲车返回到![]() 地的过程中,甲、乙两车相距190千米列出方程:80x -120(x-2.5)=190,求解即可.
地的过程中,甲、乙两车相距190千米列出方程:80x -120(x-2.5)=190,求解即可.
(1)300÷(180÷1.5)=2.5(小时),所以m=2.5小时;
![]() ,所以n=3.75小时;
,所以n=3.75小时;
(2)设甲车返回时y与x之间的函数关系式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴甲车返回时y与x之间的函数关系式是y=-100x+550(2.5≤x≤5.5);
(3)由(1)可得甲的速度:![]() ,乙的速度:
,乙的速度:![]() ,
,
设当![]() 为何值时,甲、乙两车相距190千米,
为何值时,甲、乙两车相距190千米,
若乙车未到达A地前,即![]()
根据题意可列出:80x -100(x-2.5)=190,
解得:x=3,
若乙车未到达A地前,即![]()
根据题意可列出:300-100(x-2.5)=190,
解得:x=3.6(舍去),
答:当时间为3时,甲、乙两车相距190千米.

练习册系列答案
相关题目