题目内容
【题目】已知一次函数y1=kx-2(k为常数,k≠0)和y2=x+1.
(1)当k=3时,若y1>y2,求x的取值范围.
(2)在同一平面直角坐标系中,若两函数的图像相交所形成的锐角小于15°,请直接写出k的取值范围.
【答案】(1)x>![]() ;(2)
;(2)![]() <k<
<k<![]() ,且k≠1
,且k≠1
【解析】
(1)解不等式3x-2>x+1即可;
(2)y2斜率为1,图象与x轴形成的角度为45°,若两函数的图像相交所形成的锐角小于15°,画出大致图象可判断出y1与x轴所形成的角度范围是30°到60°之间,根据特殊角的正弦值可得出k的取值范围.
解:(1)当k=3时,y1=3x-2.
根据题意,得3x-2>x+1,解得x>![]() .
.
(2)如图,
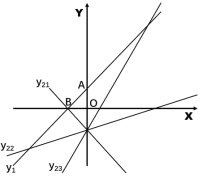
∵y2=x+1,
∴∠ABO=∠OBA=45°,
①若k<0,假设图象为y21,此时,两直线夹角一直大于45°,不符合题意,舍去;
②若k>0,假设图象为y22,此时,存在两直线夹角小于15°,由图象可得,当夹角达到最大15°时,y22与x轴夹角达到最小为30°,∴k>![]() ,当两直线平行时,无交点,此时k=1,不符合题意,舍去;当k>1时,当夹角达到最大15°时,y23与x轴夹角达到最大为60°,∴k<
,当两直线平行时,无交点,此时k=1,不符合题意,舍去;当k>1时,当夹角达到最大15°时,y23与x轴夹角达到最大为60°,∴k<![]() ,
,
综上所述,![]() <k<
<k<![]() ,且k≠1.
,且k≠1.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目