题目内容
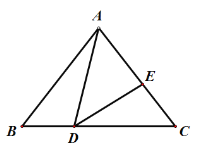
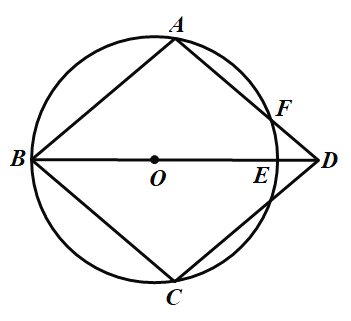
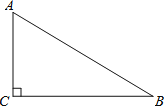
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
(2)当AC=3,BC=4时,△ACP的周长= ;
【答案】(1)见解析 (2)8
【解析】
(1)作CB的垂直平分线交BA于P点,连接PC;
(2)先利用勾股定理计算出BA=5,然后利用PC=PB可得到△ACP的周长=AC+BA=8.
(1)如图所示,作线段BC的垂直平分线交AB于点P,连接PC,点P为所求作.
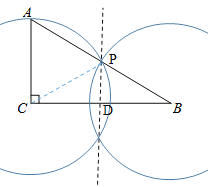
(2)∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=5,
∵PD是线段BC的垂直平分线,
∴PC=PB
∴△ACP的周长为:AC+AP+PC=AC+AP+PB=AC+AB=3+5=8.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
【题目】水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价 | 400 | 300 | 250 | 240 | 200 | 150 | 125 | 120 |
销售量 | 30 | 40 | 48 | 50 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品每天的销售量![]() (千克)与销售价格
(千克)与销售价格![]() (元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量
(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量![]() (千克)与销售价格
(千克)与销售价格(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?