题目内容
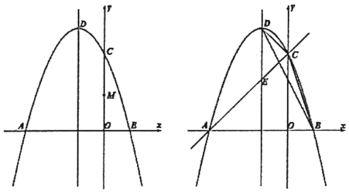
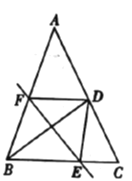
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,线段
边的中点,线段![]() 的垂直平分线分别与边
的垂直平分线分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .设
.设![]() ,
,![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() 的面积为
的面积为![]() ;③
;③![]() 的周长为
的周长为![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论有_______(把你认为正确结论的序号都填上).
.其中正确结论有_______(把你认为正确结论的序号都填上).
【答案】②⑤
【解析】
根据题意,过点A作AG⊥BC与点G,DH⊥BC于点H,先求出![]() ,
,![]() ,然后得到
,然后得到![]() 的面积,由勾股定理求出CD的长度,从而得到
的面积,由勾股定理求出CD的长度,从而得到![]() 的周长,在Rt△DEH中,由勾股定理,得到
的周长,在Rt△DEH中,由勾股定理,得到![]() ;结合题目的条件,即可得到答案.
;结合题目的条件,即可得到答案.
解:过点A作AG⊥BC与点G,DH⊥BC于点H,如图:
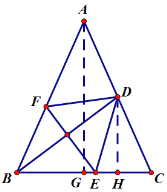
∵在![]() 中,
中,![]() ,
,![]() ,AG⊥BC,
,AG⊥BC,
∴BG=CG=6,
∵点D是AC的中点,AG∥DH,
∴CH=3,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 的面积为:
的面积为:![]() ;故②正确;
;故②正确;
由勾股定理,得![]() ,
,
∴![]() ,
,
∵EF垂直平分BD,
∴DE=BE=x,
∴![]() 的周长为
的周长为![]() ;故③错误;
;故③错误;
∵![]() ,
,
在Rt△DEH中,DE=x,DH=3y,
∴![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
根据题目的条件,不能得到![]() 和
和![]() ,故①④错误;
,故①④错误;
∴正确的结论有:②⑤;
故答案为:②⑤.

【题目】水产公司有一种海产品共2104千克,为寻求合适的销售价格,进行了8天试销,试销情况如下:
第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | 第8天 | |
售价 | 400 | 300 | 250 | 240 | 200 | 150 | 125 | 120 |
销售量 | 30 | 40 | 48 | 50 | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用反比例函数刻画这种海产品每天的销售量![]() (千克)与销售价格
(千克)与销售价格![]() (元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量
(元/千克)之间的关系.现假定在这批海产品的销售中,每天的销售量![]() (千克)与销售价格
(千克)与销售价格(元/千克)之间都满足这一关系.
(1)写出这个反比例函数的解析式;
(2)在试销8天后,公司决定将这种海产品的销售价格定为150元/千克,并且每天都按这个价格销售,那么余下的这些海产品预计再用多少天可以全部售出?
(3)在按(2)中定价继续销售15天后,公司发现剩余的这些海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新的价格销售,那么新确定的价格最高不超过每千克多少元才能完成销售任务?