Question

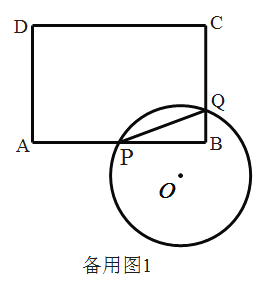
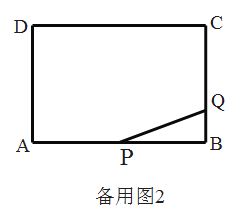
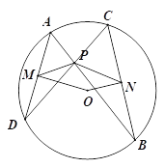
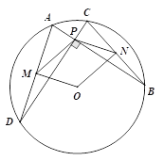
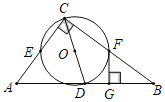
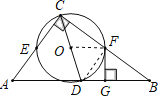
【题目】如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，连接CD，点O是CD的中点，到点O的距离等于OC的所有点组成图形M，图形M分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．

（1）试判断FG与图形M的位置关系，并说明理由；

（2）若AC＝3，∠B＝30°，求FG的长．

Answer 1

【答案】（1）FG与⊙O相切，理由详见解析；（2）FG＝．

【解析】

（1）如图，连接OF，根据直角三角形的性质得到CD＝BD，得到∠DBC＝∠DCB，根据等腰三角形的性质得到∠OFC＝∠OCF，得到∠OFC＝∠DBC，推出∠OFG＝90°，于是得到结论；

（2）连接DF，解直角三角形即可得到结论．

（1）FG与⊙O相切，

理由：根据圆的定义知：到点O的距离等于OC的所有点组成图形M，图形M就是⊙O，

如图，连接OF，

∵∠ACB＝90°，D为AB的中点，

∴CD＝BD，

∴∠DBC＝∠DCB，

∵OF＝OC，

∴∠OFC＝∠OCF，

∴∠OFC＝∠DBC，

∴OF∥DB，

∴∠OFG+∠DGF＝180°，

∵FG⊥AB，

∴∠DGF＝90°，

∴∠OFG＝90°，

∴FG与⊙O相切；

（2）连接DF，

∵∠ACB＝90°，AC＝3，∠B＝30°，

∴AB＝2AC＝6，

∴BC＝AB＝3，

∵CD为⊙O的直径，

∴∠DFC＝90°，

∴FD⊥BC，

∵DB＝DC，

∴BF＝BC＝，

∵sin∠ABC，

即，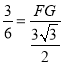

∴FG＝．