Question

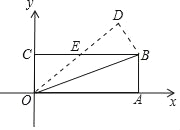
【题目】如图1，AB、CD是圆O的两条弦，交点为P.连接AD、BC. OM⊥ AD，ON⊥BC，垂足分别为M、N.连接PM、PN.

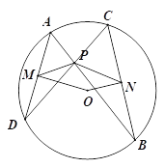
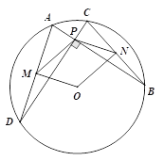
图1 图2

（1）求证：△ADP ∽△CBP；

（2）当AB⊥CD时，探究PMO与PNO的数量关系，并说明理由；

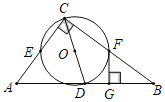
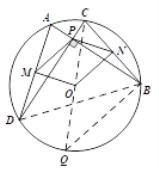
（3）当AB⊥CD时，如图2，AD=8,BC=6, ∠MON=120°，求四边形PMON的面积.

Answer 1

【答案】（1）证明见解析；（2）PMO=PNO，理由见解析；（3）S平行四边形PMON=6

【解析】

（1）利用同弧所对的圆周角相等即可证明相似,（2）由OM⊥ AD，ON⊥BC得到M、N为AB、CD的中点，再由直角三角形斜边中线等于斜边一半即可解题,（3）由三角形中位线性质得∠QBC=90°,进而证明∠QCB=∠PBD,得到四边形MONP为平行四边形即可解题.

（1）因为同弧所对的圆周角相等，所以∠A=∠C, ∠D=∠B,所以△ADP∽△CBP.

（2）PMO=PNO

因为OM⊥ AD，ON⊥BC，

所以点M、N为AB、CD的中点，

又AB⊥CD，

所以PM=AD,PN=BC，

所以，∠A=∠APM，∠C=∠CPN，

所以∠AMP=∠CNP,得到PMO与PNO.

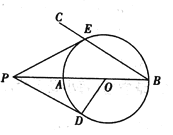
（3）连接CO并延长交圆O于点Q，连接BD.

因为AB⊥CD，AM=AD,CN=BC，

所以PM=AD,PN=BC.

由三角形中位线性质得，ON=.

因为CQ为圆O直径，所以∠QBC=90°，

则∠Q+∠QCB=90°，

由∠DPB=90°，得∠PDB+∠PBD=90°，而∠PDB=∠Q，

所以∠QCB=∠PBD,所以BQ=AD，

所以PM=ON.

同理可得，PN=OM.所以四边形MONP为平行四边形.

S平行四边形PMON=6