题目内容
【题目】在平面直角坐标系中，点A（1，0），已知抛物线y＝﹣x2+mx﹣2m（m是常数），顶点为P．
（1）当抛物线经过点A时，求顶点P坐标；
（2）等腰Rt△AOB，点B在第四象限，且OA＝OB．当抛物线与线段OB有且仅有两个公共点时，求m满足的条件；
（3）无论m取何值，该抛物线都经过定点H．当∠AHP＝45°，求此抛物线解析式．
【答案】（1）顶点P坐标(﹣
，
)；（2）m＞2
﹣3；（3）y＝﹣x2+
x﹣
或y＝﹣x2+
x﹣
【解析】
（1）将点A坐标代入解析式，可求m的值，即可求解；
（2）先求出点B坐标，由抛物线与线段OB有且仅有两个公共点，可列不等式，可求解；
（3）当x＝2时，y＝﹣4+2m﹣2m＝﹣4，则抛物线都经过定点H（2，﹣4），分点P在AH的左侧或右侧两种情况讨论，构造全等三角形，求出BH解析式，即可求解．
解：（1）∵抛物线经过点A，
∴0＝﹣1+m﹣2m，
∴m＝﹣1，
∴抛物线解析式为：y＝﹣x2﹣x+2＝﹣（x+）2+，
∴顶点P坐标（﹣，）；
（2）∵点A（1，0），OA＝OB，
∴点B（1，﹣1）
设直线OB的解析式为
将点B代入得
∴直线OB解析式为：y＝﹣x，
∵抛物线与线段OB有且仅有两个公共点，
∴﹣x＝﹣x2+mx﹣2m，
∴△＝（m+1）2﹣8m＞0，
∴m＞2﹣3，或m＜﹣2﹣3，
∵抛物线与线段OB有且仅有两个公共点，
∴
∴m≥0，
∴m＞2﹣3，
（3）∵当x＝2时，y＝﹣4+2m﹣2m＝﹣4，
∴抛物线都经过定点H（2，﹣4），
若点P在AH的左侧，如图1，过点A作AB⊥PH，过点B作BD⊥OA，过点H作HC⊥BD于C，
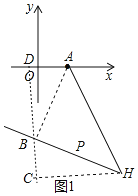
∵∠AHP＝45°，AB⊥PH，
∴∠BAH＝∠AHB＝45°，
∴AB＝BH，
∵∠DBA+∠CBH＝90°，∠DBA+∠DAB＝90°，
∴∠DAB＝∠CBH，且AB＝BH，∠ADB＝∠BCH＝90°，
∴△DAB≌△CBH（AAS）
∴AD＝BC，BD＝CH，
∵BC+BD＝4，CH﹣AD＝1，
∴BD＝CH＝
，BC＝AD＝
，
∴点B（﹣，﹣）
设直线BH解析式为：y＝kx+b，
∴
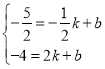
解得：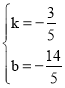
∴直线BH解析式为：y＝﹣
x﹣，
∵y＝﹣x2+mx﹣2m
∴P（
，
）
∵点P（，）在直线BH上，
∴＝﹣×﹣
∴m1＝4，m2＝，
∵当m＝4时，点P（2，﹣4）与点H重合，
∴m＝
∴抛物线解析式：y＝﹣x2+x﹣，
若点P在AH的右侧，如图2，
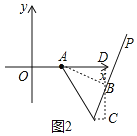
同理可求：直线BH解析式为：y＝
x﹣，
∵点P（
，）在直线BH上，
∴＝×﹣，
∴m1＝4，m2＝，
∴抛物线解析式：y＝﹣x2+x﹣，
综上所述，抛物线解析式为y＝﹣x2+x﹣或y＝﹣x2+x﹣．
