题目内容
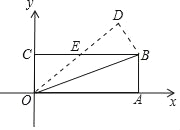
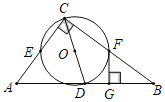
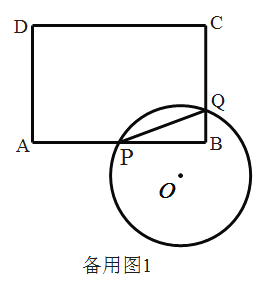
【题目】如图,已知矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点.
边上的动点.

(1)连接![]() 、
、![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() .
.
①若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() 与
与![]() 的数量关系是______;
的数量关系是______;
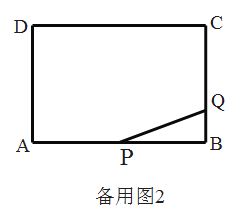
②若![]() ,求
,求![]() 的长;
的长;
(2)已知![]() ,
,![]() ,
,![]() 是以
是以![]() 为弦的圆.
为弦的圆.
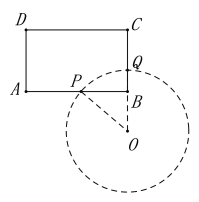
①若圆心![]() 恰好在
恰好在![]() 边的延长线上,求
边的延长线上,求![]() 的半径:
的半径:
②若![]() 与矩形
与矩形![]() 的一边相切,求
的一边相切,求![]() 的半径.
的半径.
【答案】(1)①![]() ;②1.5;(2)①5;②
;②1.5;(2)①5;②![]() 、
、![]() ,
,![]() 、5.
、5.
【解析】
(1)①根据直径所对的圆周角是直角判断△APQ为等腰三角形,结合等腰三角形的两底角相等和圆周角定理证明;②证明△PBQ∽△QBA,由对应边成比例求解;
(2)①画出图形,由勾股定理列方程求解;②分![]() 与矩形
与矩形![]() 的四边分别相切,画出图形,利用切线性质,由勾股定理列方程求解.
的四边分别相切,画出图形,利用切线性质,由勾股定理列方程求解.
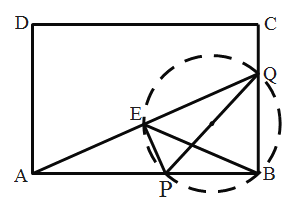
解:(1)①如图,PQ是直径,E在圆上,
∴∠PEQ=90°,
∴PE⊥AQ,
∵AE=EQ,
∴PA=PQ,
∴∠PAQ=∠PQA,
∴∠QPB=∠PAQ+∠PQA=2∠AQP,
∵∠QPB=2∠AQP.
 \
\
②解:如图,∵BE=BQ=3,
∴∠BEQ=∠BQE,
∵∠BEQ=∠BPQ,
∵∠PBQ=∠QBA,
∴△PBQ∽△QBA,
∴![]() ,
,
∴![]() ,
,
∴BP=1.5;

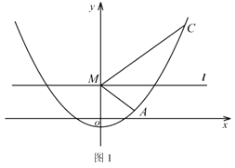
(2)①如图, BP=3,BQ=1,设半径OP=r,
在Rt△OPB中,根据勾股定理得,PB2+OB2=OP2
∴32+(r-1)2=r2,
∴r=5,
∴![]() 的半径是5.
的半径是5.
②如图,![]() 与矩形
与矩形![]() 的一边相切有4种情况,
的一边相切有4种情况,
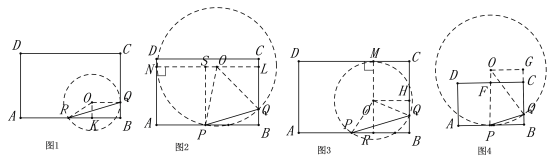
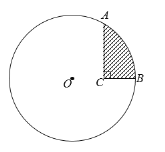
如图1,当![]() 与矩形ABCD边BC相切于点Q,过O作OK⊥AB于K,则四边形OKBQ为矩形,
与矩形ABCD边BC相切于点Q,过O作OK⊥AB于K,则四边形OKBQ为矩形,
设OP=OQ=r,则PK=3x,
由勾股定理得,r2=12+(3-r)2,
解得,r=![]() ,
,
∴![]() 半径为
半径为![]() .
.
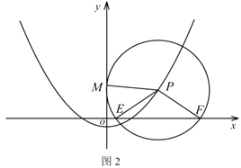
如图2,当![]() 与矩形ABCD边AD相切于点N,延长NO交BC于L,则OL⊥BC,过P作PS⊥NL于S,
与矩形ABCD边AD相切于点N,延长NO交BC于L,则OL⊥BC,过P作PS⊥NL于S,
设OS=x,则ON=OP=OQ=3+x,设PS=BL=y,
由勾股定理得,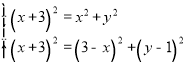 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴ON=![]() ,
,
∴![]() 半径为
半径为![]() .
.
如图3,当![]() 与矩形ABCD边CD相切于点M,延长MO交AB于R,则OR⊥AB,过O作OH⊥BC于H,
与矩形ABCD边CD相切于点M,延长MO交AB于R,则OR⊥AB,过O作OH⊥BC于H,
设OH=BR=x,设HQ=y, 则OM=OP=OQ=4-1-y=3-y,
由勾股定理得,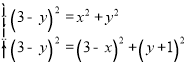 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
∴OM=![]() ,
,
∴![]() 半径为
半径为![]() .
.
如图4,当![]() 与矩形ABCD边AB相切于点P,过O作OG⊥BC于G,则四边形AFCG为矩形,
与矩形ABCD边AB相切于点P,过O作OG⊥BC于G,则四边形AFCG为矩形,
设OF=CG=x,,则OP=OQ=x+4,
由勾股定理得(x+4)2=32+(x+3)2,
解得,x=1,
∴OP=5,
∴![]() 半径为5.
半径为5.
综上所述,若![]() 与矩形
与矩形![]() 的一边相切,为
的一边相切,为![]() 的半径
的半径![]() ,
,![]() ,
,![]() ,5.
,5.