��Ŀ����
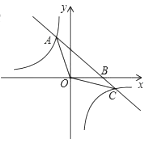
����Ŀ��һ�κ���y1��kx+1��2k��k��0����ͼ�����G1��һ�κ���y2��2x+3����1��x��2����ͼ�����G2������������ͼ�������¼���˵����
����G1��G2�й�����ʱ��y1��x�������С��
����G1��G2û�й�����ʱ��y1��x���������
����k��2ʱ��G1��G2ƽ�У���ƽ����֮��ľ���Ϊ![]() ��
��
����ѡ���У�����ȷ���ǣ�������
A.�٢���ȷ��������B.�٢���ȷ��������
C.�ڢ���ȷ��������D.�٢ڢ�����ȷ
���𰸡�D
��������
��ͼ���ҳ�G2���ٽ�㣬�Լ�G1���ٽ�ֱ�ߣ�������G1�����㣬����k�������뺯�������仯�Ĺ�ϵ����Ϻ���ͼ�����ѡ��������ɽ��
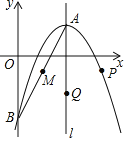
�⣺һ�κ���y2��2x+3����1��x��2���ĺ���ֵ��x�������������ͼ��ʾ��

N����1��2����Q��2��7��ΪG2�������ٽ�㣬
��֪һ�κ���y1��kx+1��2k��k��0����ͼ�������M��2��1����
ֱ��MN��ֱ��MQΪG1��G2�й�����������ٽ�ֱ�ߣ��Ӷ���G1��G2�й�����ʱ��y1��x�������С���ʢ���ȷ��
��G1��G2û�й�����ʱ�������������
һ��ֱ��MN������ʱk��0��������Ҫ��
����ֱ��MQ������ʱk�����ڣ���һ�κ������岻������MQ���������⣻
���ǵ�k��0ʱ����ʱy1��x��������������⣬�ʢ���ȷ��
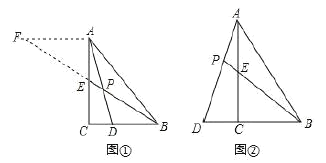
��k��2ʱ��G1��G2ƽ����ȷ������M��MP��NQ����MN��3����y2��2x+3����MN��x�ᣬ��֪��tan��PNM��2��
��PM��2PN��
�ɹ��ɶ����ã�PN2+PM2��MN2
�ࣨ2PN��2+��PN��2��9��
��PN��![]() ��
��
��PM��![]() .
.
�ʢ���ȷ��
���ϣ���ѡ��D��

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д� �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�