题目内容
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
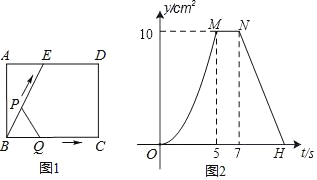
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
【答案】(1)5;(2)![]() ;
;
【解析】
(1)根据图2可得,当点P到达点E时,点Q到达点C,从而可求出BC=BE=5cm;
(2)过点P作PF⊥BC于点F,根据面积不变时△BPQ的面积为10,可得AB=4,利用三角函数求出PF的长,再结合勾股定理求解即可.
解:(1)根据图2可得,当点P到达点E时,点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm.
故答案是:5;
(2)如图1,过点P作PF⊥BC于点F,
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=![]() =
=![]() ,
,
∴PF=PBsin∠PBF=2.5×![]() =2,
=2,
∴在直角△PBF中,由勾股定理得到:BF=![]() =
=![]() =1.5,
=1.5,
∴FQ=2.5﹣1.5=1.
∴在直角△PFQ中,由勾股定理得到:PQ=![]() =
=![]() =
=![]() .
.
故答案是:![]() .
.

练习册系列答案
 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目