题目内容
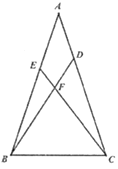
【题目】已知:在![]() 中,
中,![]() ,点D、E分别在边AC、AB上,连接BD、CE交于点
,点D、E分别在边AC、AB上,连接BD、CE交于点![]() ,且
,且![]() .
.
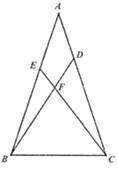
(1)求证:![]() .
.
(2)求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由等腰三角形的性质可得![]() ,即可得出∠BFC=∠DCB,由∠FBC是公共角即可证明△BCF∽△BDC;(2)由(1)得△BCF∽△BDC,根据相似三角形的性质可得
,即可得出∠BFC=∠DCB,由∠FBC是公共角即可证明△BCF∽△BDC;(2)由(1)得△BCF∽△BDC,根据相似三角形的性质可得![]() ,由∠BFC=∠EBC,∠BCF=∠ECB可证明△CFB∽△CBE,即可得△CBE∽△DCB,根据相似三角形的性质可得
,由∠BFC=∠EBC,∠BCF=∠ECB可证明△CFB∽△CBE,即可得△CBE∽△DCB,根据相似三角形的性质可得![]() ,进而可得结论.
,进而可得结论.
(1)∵AB=AC,
∴![]() ,
,
∵![]() ,
,
∴∠BFC=∠DCB,
∵![]() ,
,
∴△BCF∽△BDC.
(2)∵△BCF∽△BDC,
∴![]() ,即
,即![]() ,
,
∵∠BFC=∠EBC,∠BCF=∠ECB,
∴△CFB∽△CBE,
∴△CBE∽△DCB,
∴![]() ,即
,即![]() ,
,
∴![]()

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目