题目内容
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E、F分别在边AC、BC上)

(1)若△CEF与△ABC相似.
①当AC=BC=2时,AD的长为 ;
②当AC=3,BC=4时,AD的长为 ;
(2)当点D是AB的中点时,△CEF与△ABC相似吗?请说明理由.
【答案】解:(1)①![]() 。
。
②![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似。理由如下:
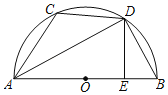
如答图3所示,连接CD,与EF交于点Q,
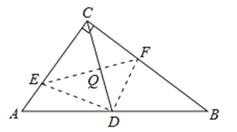
∵CD是Rt△ABC的中线,∴CD=DB=AB,∴∠DCB=∠B。
由折叠性质可知,∠CQF=∠DQF=90°,
∴∠DCB+∠CFE=90°。
∵∠B+∠A=90°,∴∠CFE=∠A。
又∵∠C=∠C,∴△CEF∽△CBA。
【解析】
(1)若△CEF与△ABC相似.
①当AC=BC=2时,△ABC为等腰直角三角形,如答图1所示,
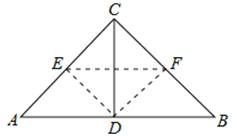
此时D为AB边中点,AD=![]() AC=
AC=![]() 。
。
②当AC=3,BC=4时,有两种情况:
(I)若CE:CF=3:4,如答图2所示,

∵CE:CF=AC:BC,∴EF∥BC。
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高。
在Rt△ABC中,AC=3,BC=4,∴BC=5。
∴cosA=![]() 。∴AD=ACcosA=3×
。∴AD=ACcosA=3×![]() =
=![]() 。
。
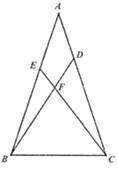
(II)若CF:CE=3:4,如答图3所示.
∵△CEF∽△CAB,∴∠CEF=∠B。
由折叠性质可知,∠CEF+∠ECD=90°。
又∵∠A+∠B=90°,∴∠A=∠ECD,∴AD=CD。
同理可得:∠B=∠FCD,CD=BD。∴AD=BD。
∴此时AD=AB=![]() ×5=
×5=![]() .
.
综上所述,当AC=3,BC=4时,AD的长为![]() 或
或![]() 。
。
(2)当点D是AB的中点时,△CEF与△ABC相似.可以推出∠CFE=∠A,∠C=∠C,从而可以证明两个三角形相似。

 阅读快车系列答案
阅读快车系列答案