Question

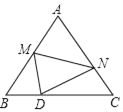
【题目】如图，等边△ABC的边长为10，点M是边AB上一动点，将等边△ABC沿过点M的直线折叠，该直线与直线AC交于点N，使点A落在直线BC上的点D处，且BD：DC=1：4，折痕为MN，则AN的长为_____．

Answer 1

【答案】7或

【解析】解：①当点A落在如图1所示的位置时，

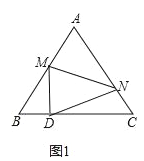
∵△ACB是等边三角形，

∴∠A=∠B=∠C=∠MDN=60°，

∵∠MDC=∠B+∠BMD，∠B=∠MDN，

∴∠BMD=∠NDC，

∴△BMD∽△CDN．

∴得，

∵DN=AN，

∴得，

∵BD：DC=1：4，BC=10，

∴DB=2，CD=8，

设AN=x，则CN=10﹣x，

∴ ，

∴DM=，BM=，

∵BM+DM=30，

∴+=10，

解得x=7，

∴AN=7；

②当A在CB的延长线上时，如图2，

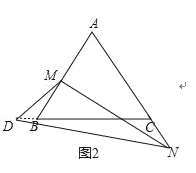
与①同理可得△BMD∽△CDN．

∴得，

∵BD：DC=1：4，BC=10，

∴DB=，CD=，

设AN=x，则CN=x﹣10，

∴ ，

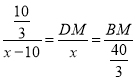∴DM=，BM=，

∵BM+DM=10，

∴+=10，

解得： x=，

∴AN=．

故答案为：7或．