Question

【题目】如图，在平面直角坐标系xOy中，二次函数y＝ax2﹣4ax+3的图象与x轴正半轴交于点A、B，与y轴相交于点C，顶点为D，且tan∠CAO＝3．

（1）求这个二次函数的解析式；

（2）点P是对称轴右侧抛物线上的点，联结CP，交对称轴于点F，当S△CDF：S△FDP＝2：3时，求点P的坐标；

（3）在（2）的条件下，将△PCD沿直线MN翻折，当点P恰好与点O重合时，折痕MN交x轴于点M，交y轴于点N，求的值．

Answer 1

【答案】（1）y＝x2﹣4x+3；（2）(5，8)；（3）

【解析】

（1）在Rt△AOC中，tan∠CAO＝＝3，求出点A的坐标，即可求解；

（2）利用，即可求解；

（3）证明∠ONM＝∠POH，则．

解：（1）∵二次函数y＝ax2﹣4ax+3的图象与y轴交于点C，

∴点C的坐标为（0，3），

∴OC＝3，

连接AC，在Rt△AOC中，tan∠CAO＝＝3，

∴OA＝1，

将点A（1，0）代入y＝ax2﹣4ax+3，得a﹣4a+3＝0，

解得：a＝1．

所以，这个二次函数的解析式为 y＝x2﹣4x+3；

（2）过点C作CG⊥DF，过点P作PQ⊥DF，垂足分别为点G、Q．

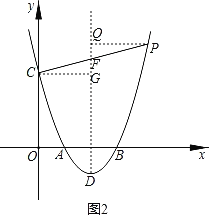
∵抛物线y＝x2﹣4x+3的对称轴为直线x＝2，

∴CG＝2，

∵，

∴PQ＝3，

∴点P的横坐标为5，

∴把x＝5代入y＝x2﹣4x+3，得 y＝8，

∴点P的坐标为（5，8）；

（3）过点P作PH⊥OM，垂足分别为点H，

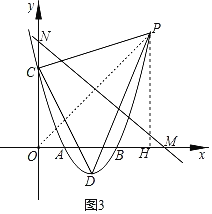
∵点P的坐标为（5，8），

∴OH＝5，PH＝8，

∵将△PCD沿直线MN翻折，点P恰好与点O重合，

∴MN⊥OP，

∴∠ONM+∠NOP＝90°，

又∵∠POH+∠NOP＝90°，

∴∠ONM＝∠POH，

∴．