题目内容
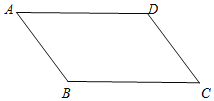
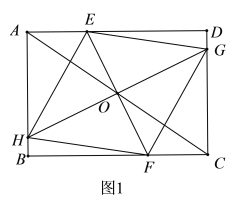
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,点
,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() 并延长交于
并延长交于![]() 点
点![]() ,过
,过![]() 作
作![]() ,分别交矩形的边于点
,分别交矩形的边于点![]()
(1)当![]() 四点分别分布在矩形
四点分别分布在矩形![]() 的四条边上(不包括顶点)时,
的四条边上(不包括顶点)时,
①求证:四边形![]() 是菱形.
是菱形.
②求![]() 的取值范围.
的取值范围.
(2)当四边形![]() 的面积为144时,求
的面积为144时,求![]() 的长.
的长.
【答案】(1)①见解析;②![]() ;(2)
;(2)![]() 为
为![]() 或
或![]() 或2或14
或2或14
【解析】
(1)①根据题意利用对角线垂直且平分的四边形是菱形判定四边形![]() 是菱形.
是菱形.
②找极限点,当![]() 与
与![]() 重合时,在
重合时,在![]() 和
和![]() 中;
中;![]() 可求得DE,进而求出AE;当
可求得DE,进而求出AE;当![]() 与
与![]() 重合时,同理可得:
重合时,同理可得:![]() ,即得到AE的取值范围;
,即得到AE的取值范围;
(2)分两种情况:
①当![]() 四边分别分布在矩形
四边分别分布在矩形![]() 的两条边上时,当点
的两条边上时,当点![]() 在边
在边![]() 上,由题(1)同理可证:四边形
上,由题(1)同理可证:四边形![]() 是菱形,且此时菱形的高为12,根据面积为144可求出
是菱形,且此时菱形的高为12,根据面积为144可求出![]() ,即四边形
,即四边形![]() 是正方形,可得到AE=2;同理当G运动到BC上时,AE=14;
是正方形,可得到AE=2;同理当G运动到BC上时,AE=14;
②当![]() 四点分别分布在矩形
四点分别分布在矩形![]() 的四条边上(不包括顶点)时,如图6.过点
的四条边上(不包括顶点)时,如图6.过点![]() 作
作![]() ,交
,交![]() 分别于点P,Q,得到
分别于点P,Q,得到![]() ,根据相似比设
,根据相似比设![]() 代入菱形面积公式求出a,再由勾股定理求出PE,即可求出
代入菱形面积公式求出a,再由勾股定理求出PE,即可求出![]() ,同理G运动到靠近C时根据对称性找出
,同理G运动到靠近C时根据对称性找出![]() .
.
解:(1)①证明:![]() 在矩形
在矩形![]() 中,
中,![]() ,
,
![]() .
.
又![]()
![]()
![]()
同理可证:![]()
又![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
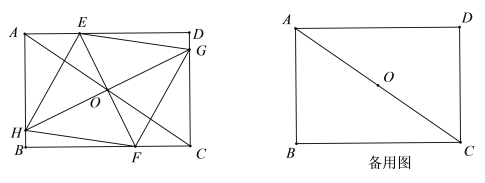
②当![]() 与
与![]() 重合时,如图2,
重合时,如图2,
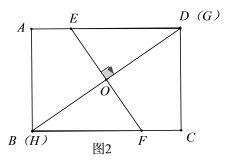
![]() 在矩形
在矩形![]() 中,
中,![]()
![]() 由勾股定理可得:
由勾股定理可得:![]() 且
且![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,
,
当![]() 与
与![]() 重合时,如图3,同理可得:
重合时,如图3,同理可得:![]() ,
,
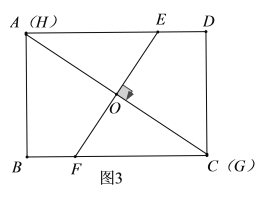
![]() ,
,
当![]() 四点分别分布在矩形
四点分别分布在矩形![]() 的四条边上(不包括顶点)时,
的四条边上(不包括顶点)时,![]() 的取值范围为
的取值范围为![]() .
.
(2)
①当![]() 四边分别分布在矩形
四边分别分布在矩形![]() 的两条边上时,当点
的两条边上时,当点![]() 在边
在边![]() 上,如图4,由题(1)同理可证:四边形
上,如图4,由题(1)同理可证:四边形![]() 是菱形,且此时菱形的高为12
是菱形,且此时菱形的高为12
![]()
![]() ,
,
![]() .
.
故![]()
![]() 四边形
四边形![]() 是正方形
是正方形
由于正方形![]() 和矩形
和矩形![]() 对称轴为同一条,
对称轴为同一条,
![]() ,
,
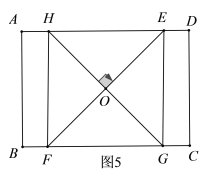
同理可证:当点![]() 在边
在边![]() 上时,如图5,
上时,如图5,![]() .
.
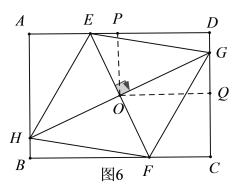
②当![]() 四点分别分布在矩形
四点分别分布在矩形![]() 的四条边上(不包括顶点)时,如图6.过点
的四条边上(不包括顶点)时,如图6.过点![]() 作
作![]() ,交
,交![]() 分别于点P,Q
分别于点P,Q
易得![]() .且
.且![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当点
当点![]() 在点
在点![]() 左侧时,
左侧时,![]() ,
,
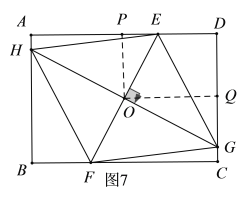
由对称性可得,当点![]() 在点
在点![]() 右侧时,如图7,
右侧时,如图7,![]() ;
;
综上所述:![]() 为
为![]() 或
或![]() 或2或14.
或2或14.