题目内容
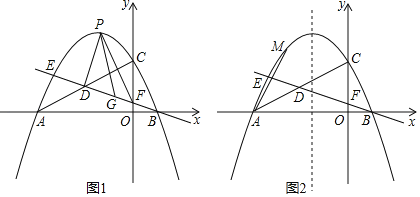
【题目】如图1,抛物线y=﹣![]() x2+bx+c的对称轴为直线x=﹣
x2+bx+c的对称轴为直线x=﹣![]() ,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
,与x轴交于点A和点B(1,0),与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求抛物线的解析式;
(2)点P是直线BE上方抛物线上一动点,连接PD、PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值.
EG的最小值.
(3)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以A、M、N、K为顶点的四边形是正方形时,请求出点N的坐标.
【答案】(1)y=﹣![]() x2+﹣
x2+﹣![]() x+2;(2)
x+2;(2)![]() ;(3)N点的坐标为:
;(3)N点的坐标为: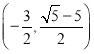 或(
或(![]() )或(﹣
)或(﹣![]() )或(﹣
)或(﹣![]() )或(﹣
)或(﹣![]() )或
)或![]() 或(﹣
或(﹣![]() )
)
【解析】
(1)根据对称轴公式列出等式,带点到抛物线列出等式,解出即可;
(2)先求出A、B、C的坐标,从而求出D的坐标算出BD的解析式,根据题意画出图形,设出P、G的坐标代入三角形的面积公式得出一元二次方程,联立方程组解出即可;
(3)分类讨论①当AM是正方形的边时,(ⅰ)当点M在y轴左侧时(N在下方), (ⅱ)当点M在y轴右侧时,②当AM是正方形的对角线时,分别求出结果综合即可.
(1)抛物线y=﹣![]() x2+bx+c的对称轴为直线x=﹣
x2+bx+c的对称轴为直线x=﹣![]() ,与x轴交于点B(1,0).
,与x轴交于点B(1,0).
∴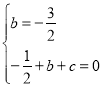 ,解得
,解得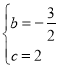 ,
,
∴抛物线的解析式为:y=﹣![]() x2+﹣
x2+﹣![]() x+2;
x+2;
(2)抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A和点B,与y轴交于点C,
x+2与x轴交于点A和点B,与y轴交于点C,
∴A(﹣4,0),B(1,0),C(0,2).
∵点D为线段AC的中点,
∴D(﹣2,1),
∴直线BD的解析式为:![]() ,
,
过点P作y轴的平行线交直线EF于点G,如图1,
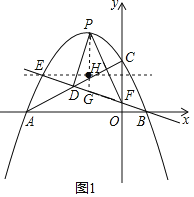
设点P(x,![]() ),则点G(x,
),则点G(x,![]() ).
).
∴![]() ,
,
当x=﹣![]() 时,S最大,即点P(﹣
时,S最大,即点P(﹣![]() ,
,![]() ),
),
过点E作x轴的平行线交PG于点H,
则tan∠EBA=tan∠HEG=![]() ,
,
∴![]() ,故
,故![]() 为最小值,即点G为所求.
为最小值,即点G为所求.
联立  解得
解得![]() ,
,![]() (舍去),
(舍去),
故点E(﹣![]() ,
,![]() ),
),
则PG﹣![]() 的最小值为PH=
的最小值为PH=![]() .
.
(3)①当AM是正方形的边时,
(ⅰ)当点M在y轴左侧时(N在下方),如图2,

当点M在第二象限时,过点A作y轴的平行线GH,过点M作MG⊥GH于点G,过点N作HN⊥GH于点H,
∴∠GMA+∠GAM=90°,∠GAM+∠HAN=90°,
∴∠GMA=∠HAN,
∵∠AGM=∠NHA=90°,AM=AN,
∴△AGM≌△NHA(AAS),
∴GA=NH=4﹣![]() ,AH=GM,
,AH=GM,
即y=﹣![]() ,/span>
,/span>
解得x=![]() ,
,
当x=![]() 时,GM=x﹣(﹣4)=
时,GM=x﹣(﹣4)=![]() ,yN=﹣AH=﹣GM=
,yN=﹣AH=﹣GM=![]() ,
,
∴N(![]() ,
,![]() ).
).
当x=![]() 时,同理可得N(
时,同理可得N(![]() ,
,![]() ),
),
当点M在第三象限时,同理可得N(![]() ,
,![]() ).
).
(ⅱ)当点M在y轴右侧时,如图3,
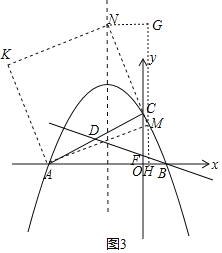
点M在第一象限时,过点M作MH⊥x轴于点H
设AH=b,同理△AHM≌△MGN(AAS),
则点M(﹣4+b,b﹣![]() ).
).
将点M的坐标代入抛物线解析式可得:b=![]() (负值舍去)
(负值舍去)
yN=yM+GM=yM+AH=![]() ,
,
∴N(﹣![]() ,
,![]() ).
).
当点M在第四象限时,同理可得N(﹣![]() ,-
,-![]() ).
).
②当AM是正方形的对角线时,
当点M在y轴左侧时,过点M作MG⊥对称轴于点G,
设对称轴与x轴交于点H,如图4.
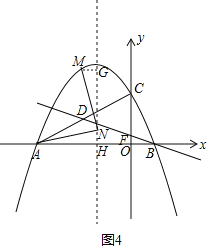
∵∠AHN=∠MGN=90°,∠NAH=∠MNG,MN=AN,
∴△AHN≌△NGN(AAS),
设点N(﹣![]() ,
,![]() ),
),
将点M的坐标代入抛物线解析式可得![]() ,
,![]() (舍去),
(舍去),
∴N(![]() ,
,![]() ),
),
当点M在y轴右侧时,同理可得N(![]() ,
,![]() ).
).
综上所述:N点的坐标为: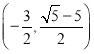 或(
或(![]() )或(﹣
)或(﹣![]() )或(﹣
)或(﹣![]() )或(﹣
)或(﹣![]() )或
)或![]() 或(﹣
或(﹣![]() ).
).