题目内容
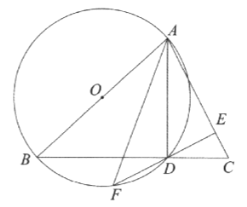
【题目】如图,E,F分别是边长为2cm的正方形ABCD的边AD,CD上的动点,满足AE=DF,连接BE,AF交于G,连接DG,则DG的最小值是_____.
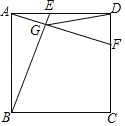
【答案】(![]() ﹣1)cm
﹣1)cm
【解析】
根据正方形的性质和已知条件,判定三角形全等,根据全等三角形的性质和直角三角形两个锐角互余的性质,得到∠AGB=90°,再利用半径所对的圆周角是90°的性质和两点间距离最短的知识,即可找到符合题意的的G点,进而利用勾股定理等即可解出答案.
解:如图,连接OD,
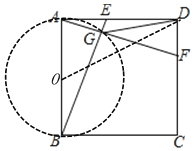
∵四边形ABCD是正方形
∴AB=AD=CD,∠BAD=90°=∠ADF
又∵AE=DF
在△ABE和△DAF中,
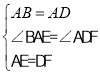
∴△ABE≌△DAF(SAS)
∴∠DAF=∠ABE
∵∠BAG+∠DAF=90°
∴∠ABE+∠BAG=90°
∴∠AGB=90°
∴点G在以AB为直径的圆O上,
∴当点G在OD上时,DG的长最小,
∴DG=OD﹣OG=![]()
故答案为:(![]() ﹣1)cm .
﹣1)cm .

练习册系列答案
相关题目