题目内容
【题目】(1)观察猜想,如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为 ;
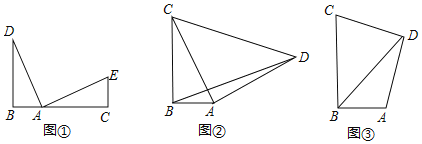
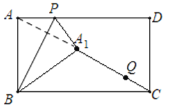
(2)问题解决,如图②,在Rt△ABC中,∠ABC=90°,CB=6,AB=3,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
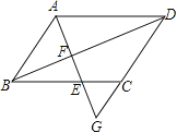
(3)拓展延伸,如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=6,AB=3,DC=DA,请直接写出BD的长.
【答案】(1)BC=BD+CE;(2)3![]() ;(3)
;(3)![]() .
.
【解析】
(1)观察猜想:证明![]() ,可得结论:
,可得结论:![]() ;
;
(2)问题解决:作辅助线,同理证明:![]() ,可得
,可得![]() ,
,![]() ,最后利用勾股定理求
,最后利用勾股定理求![]() 的长;
的长;
(3)拓展延伸:同理证明三角形全等,设![]() ,
,![]() ,根据全等三角形对应边相等列方程组可得结论.
,根据全等三角形对应边相等列方程组可得结论.
解:(1)观察猜想
结论:BC=BD+CE,理由是:
如图①,∵∠B=90°,∠DAE=90°,
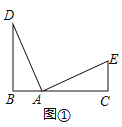
∴∠D+∠DAB=∠DAB+∠EAC=90°,
∴∠D=∠EAC,
∵∠B=∠C=90°,AD=AE,
∴△ADB≌△EAC(AAS),
∴BD=AC,EC=AB,
∴BC=AB+AC=BD+CE;
故答案为:BC=BD+CE;
(2)问题解决
如图②,过D作DE⊥AB,交BA的延长线于E,
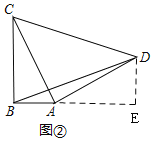
由(1)同理得:△ABC≌△DEA,
∴DE=AB=3,AE=BC=6,
Rt△BDE中,BE=9,
由勾股定理得:![]() ;
;
(3)拓展延伸
如图③,过D作DE⊥BC于E,作DF⊥AB于F,
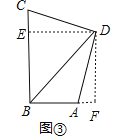
同理得:△CED≌△AFD,
∴CE=AF,ED=DF,
设AF=x,DF=y,
则![]() ,解得:
,解得:![]() ,
,
![]() ,
,![]() ,
,
由勾股定理得:![]() .
.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
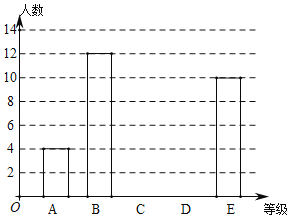
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?