��Ŀ����
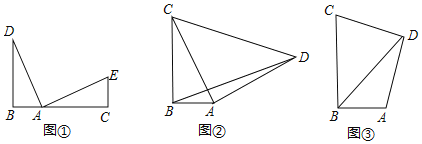
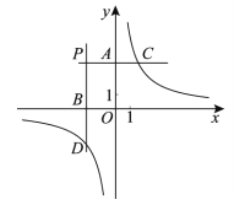
����Ŀ���������ǰ�ABC��DEF������ͼ��ʾ��λ�ðڷţ���B���D�غϣ���AB���DE��ͬһ��ֱ���ϣ�����ͼ�������еĵ㣬�߶���ͬһƽ���ڣ������У���C=��DEF=90������ABC=��F=30����AC=DE=6cm���̶ֹ����ǰ�DEF�������ǰ�ABC������DE����ƽ�ƣ�����C���ڱ�EF��ʱֹͣ�˶��������ǰ�ƽ�Ƶľ���Ϊx��cm�����������ǰ��ص����ֵ����Ϊy��cm2����

��1������C���ڱ�EF��ʱ��x= cm��
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3�����BC���е�Ϊ��M����DF���е�Ϊ��N��ֱ��д�������ǰ�ƽ�ƹ����У���M���N֮��������Сֵ��
���𰸡���1��15����2��![]()
![]()
![]() ����3��
����3��![]() ��
��
��������
��1����������Ǻ������õ�BG�ij��������ɵ�GE�ij����ɾ��ε����ʣ��ɵô𰸣�
��2���������ۣ�����0��t��6ʱ�����������ε������ʽ���ɵô𰸣�����6��t��12ʱ������12��t��15ʱ����������ĺͲ�ɵô𰸣�
��3�����ݵ���ֱ�������е�������д��߶���̣��ɵ�M���߶�NG�ϣ����������ε���λ�ߣ��ɵ�NG�ij�������������Ǻ������ɵ�MG�ij��������߶εĺͲ�ɵô𰸣�
�⣺��1����ͼ1��ʾ����CG��AB��G�㣮
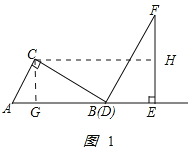 ��
��
��Rt��ABC�У���AC=6����ABC=30���ã�BC=![]() =
=![]() ����Rt��BCG�У�BG=BCcos30��=9���ı���CGEH�Ǿ��Σ�CH=GE=BG+BE=9+6=15cm���ʴ�Ϊ15��
����Rt��BCG�У�BG=BCcos30��=9���ı���CGEH�Ǿ��Σ�CH=GE=BG+BE=9+6=15cm���ʴ�Ϊ15��
��2������0��x��6ʱ����ͼ2��ʾ��
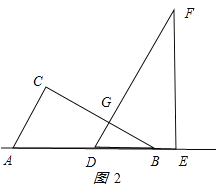 ��
��
��GDB=60������GBD=30����DB=x���ã�DG=![]() ��BG=
��BG=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() DGBG=
DGBG=![]() ��
��![]() ��
��![]() =
=![]() ��
��
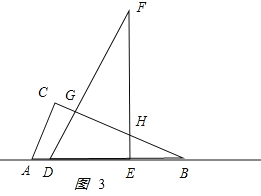
����6��x��12ʱ����ͼ3��ʾ��
 ��
��
BD=x��DG=![]() ��BG=
��BG=![]() ��BE=x��6��EH=
��BE=x��6��EH=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() =
=![]() DGBG��
DGBG��![]() BEEH����y=
BEEH����y=![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
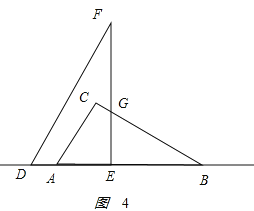
����12��x��15ʱ����ͼ4��ʾ��
 ��
��
AC=6��BC=![]() ��BD=x��BE=��x��6����EG=
��BD=x��BE=��x��6����EG=![]() ���ص����ֵ����Ϊy=
���ص����ֵ����Ϊy=![]() =
=![]() ACBC��
ACBC��![]() BEEG����y=
BEEG����y=![]() ������
������![]() =
=![]() ��
��
����������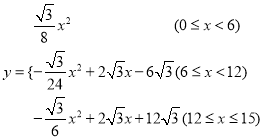 ��
��
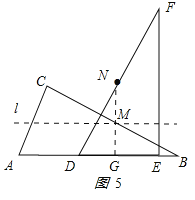
��3����ͼ5��ʾ��NG��DE��G�㣮
 ��
��
��M��NG��ʱMN��̣�NG����DEF����λ�ߣ�NG=![]() EF=
EF=![]() ��
��
MB=![]() CB=
CB=![]() ����B=30����MG=
����B=30����MG=![]() MB=
MB=![]() ��
��
MN��С=![]() =
=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�