题目内容
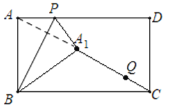
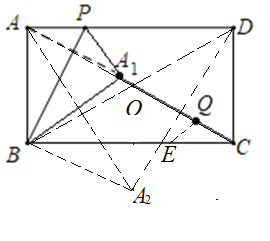
【题目】如图,在矩形ABCD中,![]() ,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
,AD=9,点P是AD边上的一个动点,连接BP,将矩形ABCD沿BP折叠,得到△A1PB,连接A1C,取A1C的三等分点Q(CQ<A1Q),当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为( )
A.πB.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接AC,BD,相交于点O,过点Q作![]() ,交BC于点E,即点E为BC的三等分点,根据平行线分线段成比例得出
,交BC于点E,即点E为BC的三等分点,根据平行线分线段成比例得出![]() 为定值,可得出点Q的运动轨迹是以点E为圆心,QE为半径的圆弧,通过对点A1运动轨迹的分析求出圆心角,最后根据弧长公式进行求解.
为定值,可得出点Q的运动轨迹是以点E为圆心,QE为半径的圆弧,通过对点A1运动轨迹的分析求出圆心角,最后根据弧长公式进行求解.
连接AC,BD,相交于点O,过点Q作![]() ,交BC于点E,即点E为BC的三等分点,
,交BC于点E,即点E为BC的三等分点,
∵在矩形ABCD中,![]() ,AD=9,
,AD=9,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵将矩形ABCD沿BP折叠,得到△A1PB,
∴![]() ,
,
∴![]() ,
,
当点P运动到点A时,点A1与点A重合,当点P运动到点D时,点A1与A2重合,此时![]() ,
,
∴点Q的运动轨迹是以点E为圆心,QE为半径,圆心角为![]() 的圆弧,
的圆弧,
∴点Q的运动路径长![]() ,
,
故选D.

练习册系列答案
相关题目