题目内容
【题目】如图所示,M为等腰三角形ABD的底边AB的中点,过D作DC∥AB,连接BC,AB=6cm,DM=3cm,DC=3-![]() cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
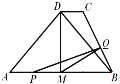
(1)当点P在线段AM上运动时,PM=_______.(用t的代数式表示)
(2)求BC的长度;
(3)当点P在MB上运动时,求S与t之间的函数关系式.
【答案】(1)PM=3-t;(2)2![]() ;(3)当3<t≤2
;(3)当3<t≤2![]() 时,S=
时,S=![]() ;当2
;当2![]() <t≤3+
<t≤3+![]() 时,S=
时,S=![]()
【解析】
(1)如图1中,根据PM=AM-AP计算即可.
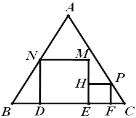
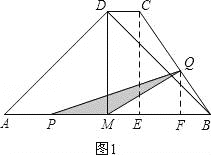
(2)过点C作CE⊥AB,垂足为E,如图2,求出EC,BE即可.
(3)分两种情形:①当![]() 时,点P在线段BM上,点Q在线段BC上,过点Q作QF⊥AB,垂足为F,如图3.②当
时,点P在线段BM上,点Q在线段BC上,过点Q作QF⊥AB,垂足为F,如图3.②当![]() 时,点P在线段BM上,点Q在线段DC上,过点Q作QF⊥AB,垂足为F,如图4,分别求解即可.
时,点P在线段BM上,点Q在线段DC上,过点Q作QF⊥AB,垂足为F,如图4,分别求解即可.
(1)如图中,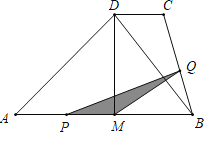
PM=3-t.
(2)过点C作CE⊥AB,垂足为E,如图1,
∵DA=DB,AM=BM,
∴DM⊥AB.
∵CE⊥AB,
∴∠CEB=∠DMB=90°.
∴CE∥DM.
∵DC∥ME,CE∥DM,∠DME=90°,
∴四边形DCEM是矩形.
∴CE=DM=3,![]() .
.
∵AM=BM,AB=6,
∴AM=BM=3.
∴![]() .
.
∵∠CEB=90°,CE=3,![]() ,
,
∴![]() .
.
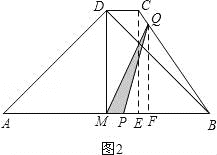
(3)①当![]() 时,点P在线段BM上,点Q在线段BC上,
时,点P在线段BM上,点Q在线段BC上,
过点Q作QF⊥AB,垂足为F,如图2,
∵QF⊥AB,CE⊥AB,
∴∠QFB=∠CEB=90°.
∴QF∥CE.
∴![]()
∴![]()
∵BQ=t,
∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]()
②当2![]() <t≤3+
<t≤3+![]() 时,点P在线段BM上,点Q在线段DC上,
时,点P在线段BM上,点Q在线段DC上,
过点Q作QF⊥AB,垂足为F,如图3,
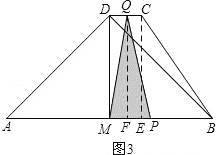
此时QF=DM=3.
∵PM=AP﹣AM=t﹣3,
∴![]()
![]()
=![]() .
.
综上所述:当3<t≤2![]() 时,S=
时,S=![]() ;当2
;当2![]() <t≤3+
<t≤3+![]() 时,S=
时,S=![]()
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案