题目内容
【题目】科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):
(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;
(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;
(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?
【答案】(1)![]() ;(2)该超市能实现A型商品的销售日净收入3000元的目的,A型商品的销售利润为17元/件或20元/件;(3)该超市A型商品的销售利润为18元/件或19元/件时,能获得A型商品的最大日净收入.
;(2)该超市能实现A型商品的销售日净收入3000元的目的,A型商品的销售利润为17元/件或20元/件;(3)该超市A型商品的销售利润为18元/件或19元/件时,能获得A型商品的最大日净收入.
【解析】
(1)根据题意可以列出相应的函数解析式;
(2)根据(1)中的函数解析式即可解答本题;
(3)根据(1)中的函数解析式即可求得y的最大值.
解:(1)由题意可得,
当0<x≤9时,y=280x﹣400,
当x>9时,y=[280﹣(x﹣9)×10]x﹣400=﹣10x2+370x﹣400,
由上可得,该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式是:y=![]() ;
;
(2)∵当0<x≤9时,y=280x﹣400≤2120,
∴令y=3000代入y=﹣10x2+370x﹣400,
解得,x1=17,x2=20,
答:该超市能实现A型商品的销售日净收入3000元的目的,A型商品的销售利润为17元/件或20元/件;
(3)∵当0<x≤9时,y=280x﹣400≤2120,
当x>9时,y=﹣10x2+370x﹣400=﹣10(x﹣![]() )2+3022.5,
)2+3022.5,
∵x>9且x为整数,
∴当x=18或19时,y取得最大值,此时y=3020,
答:该超市A型商品的销售利润为18元/件或19元/件时,能获得A型商品的最大日净收入.

【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
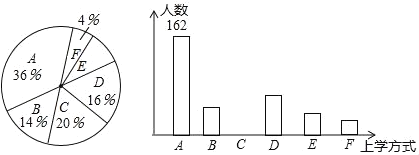
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.