题目内容
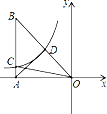
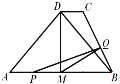
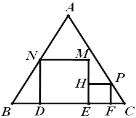
【题目】如图,正三角形ABC的边长为3+![]() ,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
,在三角形中放入正方形DEMN和正方形EFPH,使得D、E、F在边AB上,点P、N分别在边CB、CA上,设两个正方形的边长分别为m,n,则这两个正方形的面积和的最小值为( )
A. ![]() B.
B. ![]() C. 3D.
C. 3D. ![]()
【答案】D
【解析】
设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,根据等边三角形的性质得∠A=∠B=60°,利用含30度的直角三角形三边的关系得![]() ,
,![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,接着确定m的取值范围为:
,接着确定m的取值范围为:![]() ,然后根据二次函数的性质求出S的最小值.
,然后根据二次函数的性质求出S的最小值.
解:设正方形DEMN、正方形EFPH的边长分别为m、n,它们的面积和为S,
∵△ABC为等边三角形,
∴∠A=∠B=60°,![]() ,
,
在Rt△ADN中,![]() ,
,
在Rt△BPF中,![]() ,
,
∵BD+DE+EF+CF=AB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵当点M落在AC上,则正方形DEMN的边长最大,正方形EFPH的边长最小,
当点H落在BC上,则正方形DEMN的边长最小,正方形EFPH的边长最大,
∴当点M落在AC上时:
![]() 为正三角形,
为正三角形,![]()
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]()
在![]() 中,
中,![]() ,
,
∵BD+DE+EF+CF=AB,
∴![]()
解得![]() ,
,
∴![]() ,
,
∴当![]() 时,S最小,S的最小值为
时,S最小,S的最小值为![]() .
.
故选:D.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
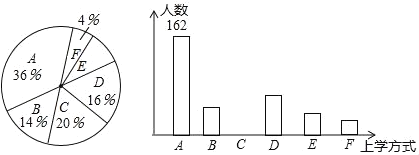
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.