题目内容
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
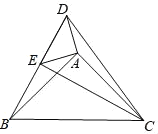
【答案】①③④
【解析】
只要证明△DAB≌△EAC,利用全等三角形的性质即可一一判断.
∵∠DAE=∠BAC=90°,∴∠DAB=∠EAC.
∵AD=AE,AB=AC,∴△DAB≌△EAC(SAS),∴BD=CE,∠ABD=∠ECA.
∵∠DCB﹣∠DCA=∠ACB=45°,显然∠ABD≠∠ACD,故②错误.
∵CE﹣BE=BD=BE=DE![]() AD,故③正确.
AD,故③正确.
∵∠ECB+∠EBC=∠ABD+∠ECB+∠ABC=45°+45°=90°,∴∠CEB=90°,即CE⊥BD,故①正确,∴BE2=BC2﹣EC2=2AB2﹣(CD2﹣DE2)=2AB2﹣CD2+2AD2=2(AD2+AB2)﹣CD2,∴BE2+CD2=2(AD2+AB2),故④正确.
故答案为:①③④.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目