题目内容
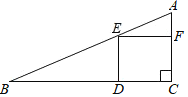
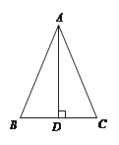
【题目】如图，△ABC中，AB＝AC，过点A作AD⊥BC于点D．
(1)确定△ABC外接圆的圆心O，并画出△ABC的外接圆⊙O；（尺规作图，保留作图痕迹，不写作法）
(2)若BC＝4，∠BAC＝45°，求⊙O的半径．
【答案】(1)作图见解析；(2)⊙O的半径为
．
【解析】
（1）作AB边的垂直平分线，相交于AD于点O，再以O为圆心，以OA长为半径画圆，⊙O即为所求的三角形的外接圆。
（2）连接BO，CO，由圆心角等于圆周角的二倍，可得∠BOC==2∠A=90°，得到△BOC是等腰直角三角形，在Rt△BOC中，利用勾股定理得⊙O的半径。
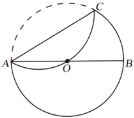
(1)如图，
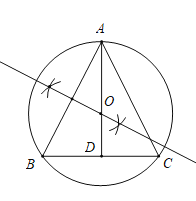
(2)连接BO，CO，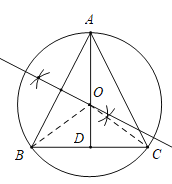
∵∠A=45°，
∴∠BOC=90°，
∴△BOC是等腰直角三角形，
∵BC=4，OB=OC
根据勾股定理得OB2+OC2=BC2
即2OB2=42．
∴OB=
即⊙O的半径为．
练习册系列答案
相关题目
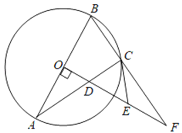
【题目】如图1，
的直径
，点
为线段
上一动点，过点作的垂线交于点
，
，连结
，
.设
的长为
，
的面积为
.
小东根据学习函数的经验，对函数
随自变量
的变化而变化的规律进行了探究.
下面是小东的探究过程，请帮助小东完成下面的问题.
（1）通过对图1的研究、分析与计算，得到了与的几组对应值，如下表：
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 0 | 0.7 | 1.7 | 2.9 |
| 4.8 | 5.2 | 4.6 | 0 |
请求出表中小东漏填的数
；
（2）如图2，建立平面直角坐标系
，描出表中各对应值为坐标的点，画出该函数的大致图象；
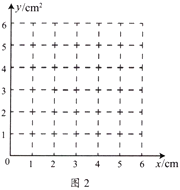
（3）结合画出的函数图象，当的面积为
时，求出的长.
