题目内容
【题目】如图，已知
的三个顶点的坐标分别为
、
、
，P（a，b）是△ABC的边AC上一点：
（1）将
绕原点
逆时针旋转90°得到
,请在网格中画出
，旋转过程中点A所走的路径长为 .
（2）将△ABC沿一定的方向平移后，点P的对应点为P2（a+6，b+2），请在网格画出上述平移后的△A2B2C2，并写出点A2、的坐标:A2（ ）.
（3）若以点O为位似中心，作△A3B3C3与△ABC成2:1的位似，则与点P对应的点P3位似坐标为 （直接写出结果).
【答案】（1）画图见解析， 
π ；（2）画图见解析，（4,4）；（3）P3 （2a，2b）或P3 （-2a，-2b）
【解析】（1）分别得出△ABC绕点O逆时针旋转90后的对应点得到
的位置，进而得到旋转后的得到
，而点A所走的路径长为以O为圆心，以OA长为半径且圆心角为90°的扇形弧长；（2）由点P的对应点为P2（a+6，b+2）可知△ABC向右平移6个单位长度，再向上平移2个单位长度，即可得到的△A2B2C2；（3）以位似比2：1作图即可，注意有两个图形，与点P对应的点P3的坐标是由P的横、纵坐标都乘以2或－2得到的.
解：（1）
如图所示，
∵
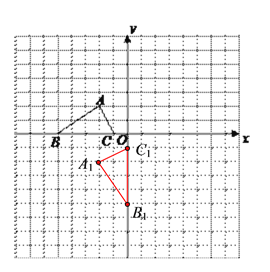
∴点A所走的路径长为： 
故答案为： 
π
（2）∵由点P的对应点为P2（a+6，b+2）
∴△A2B2C2是△ABC向右平移6个单位长度，再向上平移2个单位长度可得到的，
∴点A对应点A2坐标为（4,4）
△A2B2C2如图所示，
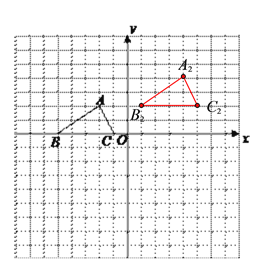
（3）∵P（a，b）且以点O为位似中心，△A3B3C3与△ABC的位似比为2:1
∴P3 （2a，2b）或P3 （-2a，-2b）
△A3B3C3如图所示，
阅读快车系列答案【题目】（10分）下面的图形是由边长为l的正方形按照某种规律排列而组成的．
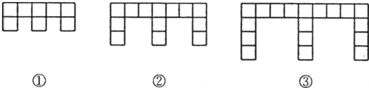
（1）观察图形，填写下表：
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
（2）推测第n个图形中，正方形的个数为 ，周长为 （都用含n的代数式表示）．
（3）这些图形中，任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= ．
