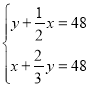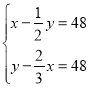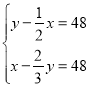题目内容
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
【答案】(1)1001;5261;(2)满足条件的“平衡数”M的值为3719.
【解析】
(1)根据平衡数的定义即可得解;
(2)根据平衡数的定义可知t=a+4,再由二次函数的性质得到a的取值范围,进而得到a的值,即可求得M的值.
(1)最小的“平衡数”为1001;
∴最大的“平衡数”为9999,
∴A=![]() ;
;
(2)设百位数字为t,则十位数字为8﹣t,
∵一个四位“平衡数”M的个位数字为3a,千位数字为a,
∴![]() ,解得t=a+4,
,解得t=a+4,
即一个四位“平衡数”M,它的千位数字围为a,百位数字为a+4,十位数字为4-a,个位数字为3a,
∵二次函数![]() 与x轴有两个交点,
与x轴有两个交点,
∴![]() 且
且![]() ,解得
,解得![]() 且a≠2,
且a≠2,
∴a=3,
∴满足条件的“平衡数”M的值为3719.

练习册系列答案
相关题目
【题目】某中学为了解七年级400名学生读书情况,随机调查了七年级50名学生读书的册数.统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均救,众数和中位数;
(2)根据样本数据,估计该校七年级400名学生在本次活动中读书多于3册的人数.