题目内容
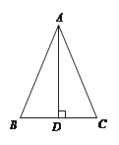
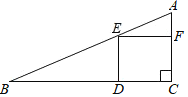
【题目】如图，在一块斜边长30cm的直角三角形木板（Rt△ACB）上截取一个正方形CDEF，点D在边BC上，点E在斜边AB上，点F在边AC上，若AF：AC＝1：3，则这块木板截取正方形CDEF后，剩余部分的面积为________
【答案】100cm2
【解析】
设AF＝x，根据正方形的性质用x表示出EF、CF，证明△AEF∽△ABC，根据相似三角形的性质求出BC，根据勾股定理列式求出x，根据三角形的面积公式、正方形的面积公式计算即可．
设AF＝x，
∵AF：AC＝1：3，
∴AC＝3x，CF＝2x，
∵四边形CDEF为正方形，
∴EF＝CF＝2x，EF∥BC，
∴△AEF∽△ABC，
∴
＝
＝
，
∴BC＝6x，
在Rt△ABC中，AB2＝AC2+BC2，即302＝（3x）2+（6x）2，
解得，x＝2
，
∴AC＝6，BC＝12，
∴剩余部分的面积＝
×12×6﹣4×4＝100（cm2）
故答案为：100cm2.
练习册系列答案
相关题目
