题目内容
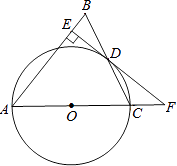
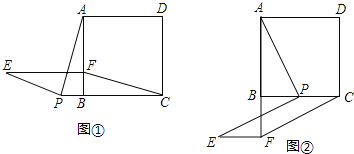
【题目】如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕 点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.
(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.
(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)由正方形的性质可以得出AB=BC,∠ABP=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论;
(2)由正方形的性质可以得出AB=BC,∠FBC=∠ABC=∠90°,可以得出△PBA≌△FBC,由其性质就可以得出结论.
试题解析:(1)证明:∵在正方形ABCD中,AB=BC,∠ABC=∠ABP=90,
又∵BF=BP,
∴△BCF≌△BAP(SAS),
∴CF=AP,∠BFC=∠BPA.
又由旋转得:∠EPA=90,PA=PE,
∴PE=CF.∵∠BFC+∠BCF=90
∴∠BPA+∠BCF=90,
∴∠BPA+∠EPA+∠BCF=180,
∴PE∥CF.
∴四边形PCFE为平行四边形.
(2)四边形PCEF是平行四边形.
证明:同(1)得:△BCF≌△BAP,
∴∠BCF=∠BAP,AP=CF.
由旋转得:AP=PE,∠EPA=90,
∴PE=CF.
∴∠BPE+∠BPA=90,
∵在△ABP中,∠ABP=90
∴∠BAP+∠BPA=90,∠BPE=∠BAP,
∴∠BPE=∠BCF,
∴PE∥CF,
∴四边形PCFE为平行四边形.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目