题目内容
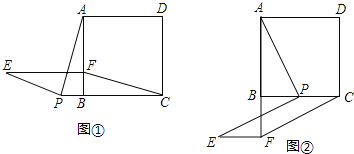
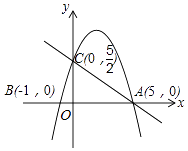
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0, ![]() ).
).
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得△ACP是以点A为直角顶点的直角三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点G为抛物线上的一动点,过点G作GE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点G的坐标.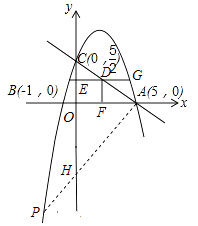
【答案】
(1)
解:∵抛物线y=ax2+bx+c与x轴交于A(5,0),B(﹣1,0)两点,与y轴交于点C(0, ![]() ),
),
∴设抛物线的解析式是y=a(x﹣5)(x+1)1),
则 ![]() =a×(﹣5)×1,解得a=﹣
=a×(﹣5)×1,解得a=﹣ ![]() .
.
则抛物线的解析式是y=﹣ ![]() (x﹣5)(x+1)=﹣
(x﹣5)(x+1)=﹣ ![]() x2+2x+
x2+2x+ ![]()
(2)
解:存在.
当点A为直角顶点时,过A作AP⊥AC交抛物线于点P,交y轴于点H,如图.
∵AC⊥AP,OC⊥OA,
∴△OAC∽△OHA,
∴ ![]() =
= ![]() ,
,
∴OA2=OCOH,
∵OA=5,OC= ![]() ,
,
∴OH=10,
∴H(0,﹣10),A(5,0),
∴直线AP的解析式为y=2x﹣10,
联立 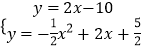 ,
,
∴P的坐标是(﹣5,﹣20).
(3)
解:∵DF⊥x轴,DE⊥y轴,
∴四边形OFDE为矩形,
∴EF=OD,
∴EF长度的最小值为OD长度的最小值,
当OD⊥AC时,OD长度最小,
此时S△AOC= ![]() ACOD=
ACOD= ![]() OAOC,
OAOC,
∵A(5,0),C(0, ![]() ),
),
∴AC= ![]() ,
,
∴OD= ![]() ,
,
∵DE⊥y轴,OD⊥AC,
∴△ODE∽△OCD,
∴ ![]() =
= ![]() ,
,
∴OD2=OECO,
∵CO= ![]() ,OD=
,OD= ![]() ,
,
∴OE=2,
∴点G的纵坐标为2,
∴y=﹣ ![]() x2+2x+
x2+2x+ ![]() =2,
=2,
解得x1=2﹣ ![]() ,x2=2+
,x2=2+ ![]() ,
,
∴点G的坐标为(2﹣ ![]() ,2)或(2+
,2)或(2+ ![]() ,2).
,2).
【解析】(1)运用待定系数法就可求出抛物线的解析式;(2)以A为直角顶点,根据点P的纵、横坐标之间的关系建立等量关系,就可求出点P的坐标;(3)连接OD,易得四边形OFDE是矩形,则OD=EF,根据垂线段最短可得当OD⊥AC时,OD(即EF)最短,然后只需求出点D的纵坐标,就可得到点P的纵坐标,就可求出点P的坐标.

【题目】节能电动车越来越受到人们的喜欢,新开发的各种品牌电动车相继投入市场.小李车行经营的A型节能电动车2015年销售总额为m万元,2016年每辆A型节能电动车的销售价比2015年降低2000年,若2015年和2016年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则2016年的销售总额比2015年减少20%.
(1)2016年A型节能电动车每辆售价多少万元?(用列方程方法解答)
(2)小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且2016年A,B两种型号节能电动车的进货和销售价格如表,那么2016年新款B型节能电动车至少要购进多少辆?
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 2016年的销售价格 | 2 |