��Ŀ����
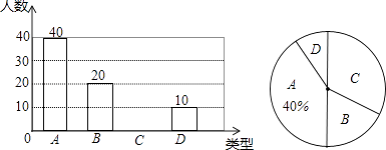
����Ŀ��ijУ�ڡ�6��26���ʽ����ա�ǰ��֯���꼶ȫ��ѧ��320�˽�����һ�Ρ���ƷԤ��֪ʶ�����������������ȡ�˲���ѧ���ɼ�����ͳ�ƣ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ�����ṩ����Ϣ������������⣺


��1������![]() ��___��
��___�� ![]() ��____������ȫֱ��ͼ��
��____������ȫֱ��ͼ��
��2����������ͳ��ͼ�����˳ɼ�ͳ�Ʒֲ�������������80��![]() ��100��Ӧ���ε�Բ�ĽǶ�����___��
��100��Ӧ���ε�Բ�ĽǶ�����___��
��3������Ƹ��꼶������60��![]() ��70��ѧ���ж����ˣ�
��70��ѧ���ж����ˣ�
���𰸡���1������������2����2��144�㣻��3��64��
�������������������1����������������������ɵó�a��b��ֵ����ȫֱ��ͼ���ɣ�
��2����360����80��x��100��Ƶ�ʼ��ɵó��𰸣�
��3��ȫУ��������60![]() ��70�ֵ�ѧ��Ƶ�ʼ��ɣ�
��70�ֵ�ѧ��Ƶ�ʼ��ɣ�
�����������1���ߵ�����������ǣ�4��0.1=40���ˣ�
��a=40��0.2=8���ˣ���
b=12��40=0.3��
��ȫֱ��ͼ��ͼ��ʾ��
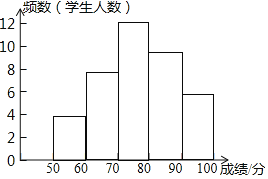
�ʴ�Ϊ��8��0.3��
��2��������80��x��100��Ӧ���ε�Բ�ĽǶ����ǣ�
360�����0.25+0.15��=144����
�ʴ�Ϊ��144����
��3����������ã�
320��0.2=64���ˣ���
�𣺹��Ƹ��꼶������60��x��100��ѧ����64�ˣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮