题目内容
【题目】如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F. 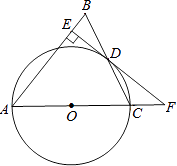
(1)求证:EF是⊙O的切线;
(2)若EB= ![]() ,且sin∠CFD=
,且sin∠CFD= ![]() ,求⊙O的半径与线段AE的长.
,求⊙O的半径与线段AE的长.
【答案】
(1)证明:连结OD,如图,
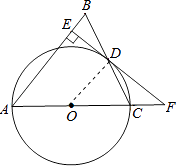
∵AB=AC,
∴∠B=∠ACD,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠B=∠ODC,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:在Rt△ODF,sin∠OFD= ![]() =
= ![]() ,
,
设OD=3x,则OF=5x,
∴AB=AC=6x,AF=8x,
在Rt△AEF中,∵sin∠AFE= ![]() =
= ![]() ,
,
∴AE= ![]() 8x=
8x= ![]() x,
x,
∵BE=AB﹣AE=6x﹣ ![]() x=
x= ![]() x,
x,
∴ ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,
,
∴AE= ![]()
![]() =6,
=6,
OD=3 ![]() =
= ![]() ,
,
即⊙O的半径长为 ![]() .
.
【解析】(1)连结OD,如图,由AB=AC得到∠B=∠ACD,由OC=OD得到∠ODC=∠OCD,则∠B=∠ODC,于是可判断OD∥AB,然后利用DE⊥AB得到OD⊥EF,然后根据切线的判定定理得到结论;(2)在Rt△ODF利用正弦的定义得到sin∠OFD= ![]() =
= ![]() ,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE=
,则可设OD=3x,OF=5x,所以AB=AC=6x,AF=8x,在Rt△AEF中由于sin∠AFE= ![]() =
= ![]() ,可得到AE=
,可得到AE= ![]() x,接着表示出BE得到
x,接着表示出BE得到 ![]() x=
x= ![]() ,解得x=
,解得x= ![]() ,于是可得到AE和OD的长.
,于是可得到AE和OD的长.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目