题目内容
过 O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.
O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.

 O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.
O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.
证明见解析.
试题分析:先连接BC,AB,由圆周角的性质就可以得出BC=AB,再证明△BFC≌△BEA就可以得出结论.
试题解析:连接BA、BC,

∵∠AMB=∠BMC,
∴AB=CB.
∵BE⊥MA,BF⊥MC,
∴BE=BF.
在Rt△ABE和Rt△CBF中,
 ,
,∴Rt△ABE≌Rt△CBF,
∴AE=CF.
考点: 1.全等三角形的判定与性质;2.角平分线的性质;3.圆心角、弧、弦的关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目


 ,BP=6,AP=
,BP=6,AP= ,求QC的长.
,求QC的长.
 ,弦AC=
,弦AC= ,点P为半圆O上一点(不与点A、C)重合. 则∠APC的度数为 .
,点P为半圆O上一点(不与点A、C)重合. 则∠APC的度数为 .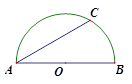
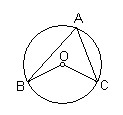
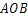 的半径为
的半径为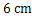 ,圆心角的度数为
,圆心角的度数为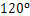 ,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为 .
,若将此扇形围成一个圆锥,则围成的圆锥的侧面积为 .