题目内容
半径为6cm和4cm的两圆相切，则它们的圆心距为（ ）
| A．2cm | B．5cm | C．2cm或5cm | D．2cm或10cm |
D.
试题分析：已知两圆的半径，分两种情况：①当两圆外切时；②当两圆内切时；即可求得两圆的圆心距．
∵两圆半径分别为3cm和2cm，
∴当两圆外切时，圆心距为6+4=10cm；
当两圆内切时，圆心距为6-4=2cm．
故选D．
考点: 圆与圆的位置关系．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
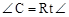，以顶点C为圆心，BC为半径作圆. 若
.
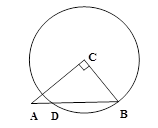
AB求点O与AB的距离．
．
O上一点M作弦MA、MB、MC，使∠AMB=∠BMC，过B作BE⊥MA于E，BF⊥MC于F，求证：AE=CF.
