题目内容
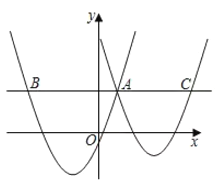
【题目】已知抛物线y=![]() 的图像与
的图像与![]() 轴的一个交点为A(-1,0),另一个交点为B,与
轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴交于点C(0,﹣3),顶点为D.
轴交于点C(0,﹣3),顶点为D.
(1)求二次函数的解析式和点D的坐标;
(2)若点M是抛物线在![]() 轴下方图像上的一动点,过点M作MN∥
轴下方图像上的一动点,过点M作MN∥![]() 轴交线段BC于点N,当MN取最大值时,点M 的坐标;
轴交线段BC于点N,当MN取最大值时,点M 的坐标;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点D落在x轴上,原抛物线上一点P平移后的对应点为Q,如果∠OQP=∠OPQ,试求点Q的坐标.
【答案】(1)抛物线的解析式为y=x2﹣2x﹣3,顶点D(1,﹣4);(2)点M的坐标为(![]() ,
,![]() );(3)Q(
);(3)Q(![]() ,2)或(
,2)或(![]() ,2)
,2)
【解析】
(1)把点A(-1,0),C(0,﹣3)代入解析式求解,然后化为顶点式即可;
(2)由(1)的解析式求出函数与x轴的交点坐标,即可得到B(3,0),根据已知条件求出直线BC的解析式![]() ,根据M在二次函数的图像上,N在一次函数图像上,可设两个点的坐标为M
,根据M在二次函数的图像上,N在一次函数图像上,可设两个点的坐标为M ![]() ,N
,N![]() ,可得MN
,可得MN ![]() ,得到关于m的方程,化为顶点式即可得到结果;
,得到关于m的方程,化为顶点式即可得到结果;
(3)先根据顶点在x轴上确定函数平移的距离,再根据∠OQP=∠OPQ得到OP=OQ,即可得到结果.
解:(1)∵抛物线y=![]() 经过A(-1,0),C(0,﹣3);
经过A(-1,0),C(0,﹣3);
得![]() ;
;
∴![]() ;
;
∴抛物线的解析式为y=x2﹣2x﹣3;
∴y=(x﹣1)2﹣4;
∴顶点D(1,﹣4).
(2)∵y=x2﹣2x﹣3;
当 y=0时,x2﹣2x﹣3=0;
解得 ![]() ,
,![]() ;
;
∴B(3,0).
设直线BC解析式为y=kx+b(k≠0);
把B(3,0)、C(0,-3)代入y=kx+b;
可得![]() ;
;
解得:![]() ;
;
∴直线BC解析式为![]() ;
;
设M ![]() ,N
,N![]() ;
;
∴MN ![]()
![]()
![]() ;
;
∴当MN最大时,点M的坐标为(![]() ,
,![]() ).
).
(3)由(1)可得抛物线顶点坐标D(1,﹣4),根据题意可得抛物线向上平移4个单位长度;
∵点P在原抛物线y=x2﹣2x﹣3上;
∴设P(x, x2﹣2x﹣3),则Q(x, x2﹣2x+1);
∵∠OQP=∠OPQ;
∴OP=OQ;
∴得到![]() 或
或![]() ;
;
∴Q(![]() ,2)或(
,2)或(![]() ,2).
,2).