题目内容
【题目】如图，一艘快艇从O港出发，向西北方向行驶到M处，然后向正东行驶到N处，再向西南方向行驶，共经过1.5小时回到O港，已知快艇的速度是每小时50海里，则M，N之间的距离是（ ）海里
A.75
﹣75B.
C.75D.50
【答案】A
【解析】
先证出△MON为等腰直角三角形，OM＝ON＝
MN，根据题意可得OM+OM+MN＝75，由此即可求得M，N之间的距离．
如图所示：
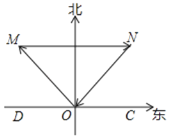
由题意得：∠NOC＝45°，∠MOD＝45°，
∴∠MON＝90°，
∵MN∥x轴，
∴∠MNO＝∠NOC＝45°，∠NMO＝∠MOD＝45°，
∴△MON为等腰直角三角形，
∴OM＝ON＝MN，
∵OM+OM+MN＝50×1.5＝75（海里），
∴MN+MN+MN＝75，
解得：MN＝（75
﹣75）海里，
即M，N之间的距离是（75﹣75）海里；
故选：A．
【题目】为增强学生垃圾分类意识，推动垃圾分类进校园．某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”，为了解学生的答题情况，学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析．
（1）学校设计了以下三种抽样调查方案：
方案一：从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析；
方案二：从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析；
方案三：从三个年级全体学生中随机抽取部分学生成绩进行调查分析．
其中抽取的样本具有代表性的方案是__________．（填“方案一”、“方案二”或“方案三”）
（2）学校根据样本数据，绘制成下表（90分及以上为“优秀”，60分及以上为“及格”）：
样本容量 | 平均分 | 及格率 | 优秀率 | 最高分 | 最低分 |
100 | 93.5 |
|
| 100 | 80 |
分数段统计（学生成绩记为 | |||||
分数段 |
|
|
|
|
|
频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题：
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内；
②估计该校1200名学生中达到“优秀”的学生总人数．
