Question

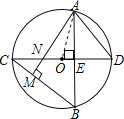
【题目】如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD．AB=，ON=1，则⊙O的半径长为_____________．

Answer 1

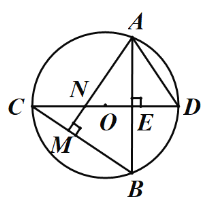
【答案】3

【解析】

先根据圆周角定理得出∠BAD=∠BCD，再由直角三角形的性质得出∠ANE=∠CNM，故可得出∠BCD=∠BAM，由全等三角形的判定定理得出△ANE≌△ADE，得到NE=ED，根据垂径定理求出AE的长，设NE=，则OE=，NE=ED=，r=OD=OE+ED=，连结AO，则AO=OD=，在Rt△AOE中根据勾股定理可得出的值，进而得出结论．

∵∠BAD与∠BCD是同弧所对的圆周角，
∴∠BAD=∠BCD，
∵AE⊥CD，AM⊥BC，
∴∠AMC=∠AEN=90°，
∵∠ANE=∠CNM，
∴∠BCD=∠BAM，
∴∠BAM=BAD，
在△ANE与△ADE中，

，

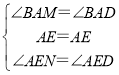∴△ANE≌△ADE，
∴NE=ED，

∵AB=，AE⊥CD，
∴AE=AB =，

又∵ON=1，
∴设NE=，则OE=，NE=ED=，，
连结AO，

∴AO=OD=，
∵△AOE是直角三角形，AE=，，OE=，AO=，

∴，即，

整理得：，

解得：(舍去)，

∴．

故答案为：．