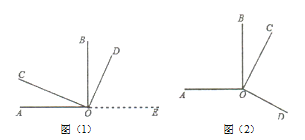Question

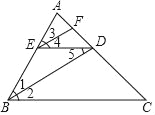
【题目】已知，点A，点B分别在线段MN，PQ上∠ACB﹣∠MAC＝∠CBP

（1）如图1，求证：MN∥PQ；

（2）分别过点A和点C作直线AG、CH使AG∥CH，以点B为顶点的直角∠DBI绕点B旋转，并且∠DBI的两边分别与直线CH，AG交于点F和点E，如图2试判断∠CFB、∠BEG是之间的数量关系，并证明；

（3）在（2）的条件下，若BD和AE恰好分别平分∠CBP和∠CAN，并且∠ACB＝60°，求∠CFB的度数．

Answer 1

【答案】（1）见解析；（2）∠CFB﹣∠BEG＝90°，证明见解析；（3）∠CFB＝120°．

【解析】

（1）过C作CE∥MN，根据平行线判定和性质证出CE∥PQ；（2）过B作BR∥AG，根据平行线判定和性质证出∠BEG＝90°﹣∠RBF＝90°﹣（180°﹣∠CFB）；（3）过B作BR∥AG，根据平行线判定和性质证出∠NAE＝∠AES，∠QBE＝∠EBC，根据角平分线定义得：∠CAE＝∠AES，再证∠AEB＝∠AES+∠BES＝∠CAE+∠CBE＝，∠AEB＝150°，∠BEG＝30°.

（1）过C作CE∥MN，

∴∠1＝∠MAC，

∵∠2＝∠ACB﹣∠1，

∴∠2＝∠ACB﹣∠MAC，

∵∠ACB﹣∠MAC＝∠CBP，

∴∠2＝∠CBP，

∴CE∥PQ，

∴MN∥PQ；

（2）过B作BR∥AG，

∵AG∥CH，

∴BR∥HF，

∴∠BEG＝∠EBR，∠RBF+∠CFB＝180°，

∵∠EBF＝90°，

∴∠BEG＝∠EBR＝90°﹣∠RBF，

∴∠BEG＝90°﹣∠RBF＝90°﹣（180°﹣∠CFB），

∴∠CFB﹣∠BEG＝90°；

（3）过E作ES∥MN，

∵MN∥PQ，

∴ES∥PQ，

∴∠NAE＝∠AES，∠QBE＝∠EBC，

∵BD和AE分别平分∠CBP和∠CAN，

∴∠NAE＝∠EAC，∠CBD＝∠DBP，

∴∠CAE＝∠AES，

∵∠EBD＝90°，

∴∠EBQ+∠PBD＝∠EBC+∠CBD＝90°，

∴∠QBE＝∠EBC，

∴∠AEB＝∠AES+∠BES＝∠CAE+∠CBE＝，

∵∠ACB＝60°，

∴∠AEB＝150°，

∴∠BEG＝30°，

∵∠CFB﹣∠BEG＝90°，

∴∠CFB＝120°．